book.mathe.studien.cloud

Polynomdivision¶

Handwerkszeug für dieses Notebook:¶

Rechenoperationen:

Multiplikation: *

Division und Brüche: /

Eingabe von Potenzen: **

Eingabe eines Kommas als Punkt: .

Eine Zelle ausführen: Enter und Shift gleichzeitig

Wurzeln: Quadratwurzeln: $\sqrt{x} =$ sqrt(x) und n-te Wurzeln: $\sqrt[n]{x} =$ x**(1/n)

$e$ -Funktion: $e^x$ = exp(x)

Logarithmen: ln(x) bzw. log(x)

Egal, wo Sie sich im Notebook befinden: Wenn Sie Fragen zur Eingabe haben, können Sie einfach eine Zelle generieren, dort Spickzettel() eintragen und die Zelle durch gleichzeitiges Drücken der Shift und der Enter-Taste ausführen. Daraufhin erscheint noch einmal eine Liste mit Hinweisen, wie was eingegeben werden muss. Probieren Sie das gerne gleich einmal aus, indem Sie die nächste Zelle auführen.

# Führen Sie diese Zelle aus. Damit erhalten Sie nochmal alle Hinweise zu den nötigen Eingaben
Spickzettel()

Polynommultiplikation¶

$ax^2 +bx +c = 0$ und $a \cdot (x-x_1) \cdot (x-x_2) = 0$ mit $x_1, x_2 \in \mathbb{R}$ stellen quadratische Gleichungen dar und

$f(x) = ax^2 +bx +c$ und $f(x) = a \cdot (x-x_1) \cdot (x-x_2)$ haben die Formen von quadratischen Funktionen.

Die Lösung einer quadratischen Gleichung sowie die Nullstellen einer quadratischen Funktion werden mit Hilfe der Mitternachtsformel oder in der Produktform durch Ablesen bestimmt.

Multipliziert man die Gleichung $a \cdot (x-x_1) \cdot (x-x_2) = 0$ mit $(x-x_3)$ ergibt sich eine Gleichung dritten Grades $a \cdot (x-x_1) \cdot (x-x_2) \cdot (x-x_3) = 0$ .

Dasselbe gilt für eine quadratische Funktion $f(x) = a \cdot (x-x_1) \cdot (x-x_2)$ : Multipliziert man diese mit $(x-x_3)$ ergibt sich eine Funktion dritten Grades mit $g(x) = a \cdot (x-x_1) \cdot (x-x_2) \cdot (x-x_3)$

Dabei spricht man von Polynommultiplikation.

Weitere Beispiele, wie eine Gleichung dritten Grades aussehen kann, sind:
$a \cdot (x^2 + 2x + 1) (x-x_3) =$
$a \cdot (x+1)(x+1)(x-x_3) =$
$a \cdot (x+1)^2 (x-x_3)$

Das gilt auch für die Form von Funktionen dritten Grades.

Polynomdivision¶

Wie können nun also Gleichungen dritten oder höheren Grades gelöst oder die Nullstellen von Funktionen dritten oder höheren Grades bestimmt werden?

Hierfür wird die Polynomdivision benötigt.

Gegeben sei die Gleichung $x^3 + 6x^2 + 9x +4 = 0$

Gesucht sind die Lösungen der Gleichung.

Vorgehensweise zur Lösung von Gleichungen dritten Grades sowie zur Bestimmung von Nullstellen einer Funktion dritten Grades:

Eine Lösung durch Probieren finden.
Polynomdivision durchführen
Verbleibende quadratische Gleichung lösen wie in 02_Quadratische_Gleichungen.ipynb

Die Vorgehensweise zur Durchführung einer Polynomdivision wird im Video https://youtu.be/x4Qvic5B-Lo an einem Beispiel gezeigt!

Lösung der Gleichung: $x^3 + 6x^2 + 9x +4 = 0$

Lösung durch Probieren finden:

Man probiert verschiedene Zahlen durch, ob diese die Gleichung erfüllen. Am besten beginnt man mit 1 und -1.

für

x = 1

:

1^3 + 6 \cdot 1^2 + 9 \cdot 1 + 4 = 20 ≠ 0

für $x= -1$ : $(-1)^3 + 6 \cdot (-1)^2 + 9 \cdot (-1) + 4 = 0$

Eine Lösung der Gleichung ist damit $x = -1$

Oben, im Abschnitt Polynommultiplikation, wurde eine quadratische Gleichung $a \cdot (x-x_1) \cdot (x-x_2) = 0$ mit einem Term $(x - x_3)$ multipliziert. $x_3$ ist eine direkt ablesbare Lösung der Gleichung. Die hier durch Probieren bestimmte Lösung $x = -1$ kann verwendet werden, um die Gleichung $x^3 + 6x^2 + 9x +4 = 0$ durch $(x + 1)$ zu dividieren. Es handelt sich hiermit um die umgekehrte Rechenoperation zur Polynommulitplikation, die Polynomdivision. Diese folgt im nächsten Schritt.

Polynomdivision durchführen:

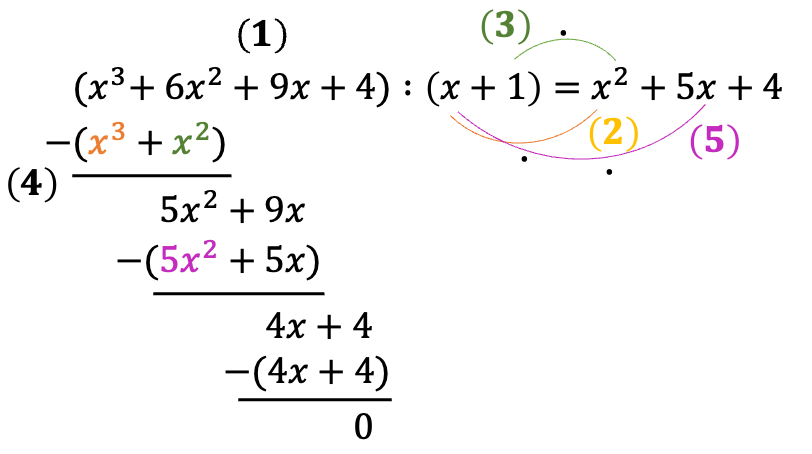
Beschreibung des Rechenverfahrens:
$\color{black}1$ . Falls noch nicht geschehen, werden die Summenglieder innerhalb beider Klammern nach der Variablen mit der höchsten Potenz in absteigender Reihenfolge geordnet.
$\color{orange}2.$ Das erste Summenglied der linken Klammer wird durch das erste Summenglied der rechten Klammer dividiert.
$\color{green}3$ . Das Ergebnis aus 2. wird mit der rechten Klammer multipliziert. $\color{green}$
4. Das Ergebnis aus 3. wird von der linken Klammer abgezogen.
$\color{purple}5$ . Das erste Summenglied des Ergebnisses aus 4. wird wieder durch das erste Summenglied der rechten Klammer dividiert.
6. Die Schritte werden so lange wiederholt bis alle Summenglieder aus der linken Klammer durch die Summenglieder der rechten Klammer dividiert wurden.

Quadratische Gleichung lösen:

Die verbleibende quadratische Gleichung $x^2 + 5x +4$ kann mit der $p-q-$ Formel oder der Mitternachtsformel gelöst werden.

Für die quadratische Gleichung ergeben sich die Lösungen $x_2 = -1$ und $x_3 = -4$ .

Damit hat die Gleichung $x^3 + 6x^2 + 9x +4 = 0$ die Lösungen
$x_1 = -1$
$x_2 = -1$
$x_3 = -4$
und kann auch umgeschrieben werden zu: $(x + 1) \cdot (x + 1) \cdot (x+4) = 0$

Polynomdivision mit Rest¶

Im oberen Beispiel bleibt bei der Polynomdivision kein Rest. Geht die Rechnung jedoch nicht auf, wird der Rest folgendermaßen hinten angeschrieben:

Beispiel: $(4x^5 - x^4 + 2x^3 + x^2 - 1) : (x^2 + 1)$

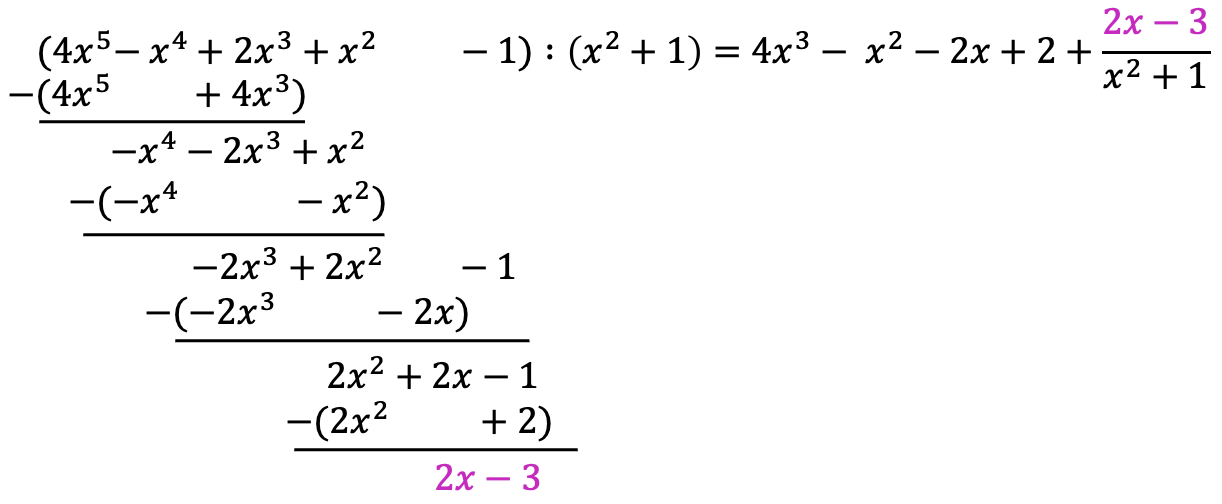
Dies ist ebenso ein Beispiel dafür, dass die Polynomdivision nicht nur für Gleichungen dritten, sondern auch höheren Grades angewandt werden kann.