Funktionen¶
Handwerkszeug für dieses Notebook:¶
Rechenoperationen:
Multiplikation: *
Division und Brüche: /
Eingabe von Potenzen: **
Eingabe eines Kommas als Punkt: .
Eine Zelle ausführen: Enter und Shift gleichzeitig
Wurzeln: Quadratwurzeln: sqrt(x) und n-te Wurzeln: x**(1/n)
-Funktion: = exp(x)
Logarithmen: ln(x) bzw. log(x)
Egal, wo Sie sich im Notebook befinden: Wenn Sie Fragen zur Eingabe haben, können Sie einfach eine Zelle generieren, dort Spickzettel() eintragen und die Zelle durch gleichzeitiges Drücken der Shift und der Enter-Taste ausführen. Daraufhin erscheint noch einmal eine Liste mit Hinweisen, wie was eingegeben werden muss. Probieren Sie das gerne gleich einmal aus, indem Sie die nächste Zelle auführen.
# Führen Sie diese Zelle aus. Damit erhalten Sie nochmal alle Hinweise zu den nötigen Eingaben
Spickzettel()Lineare Funktionen¶
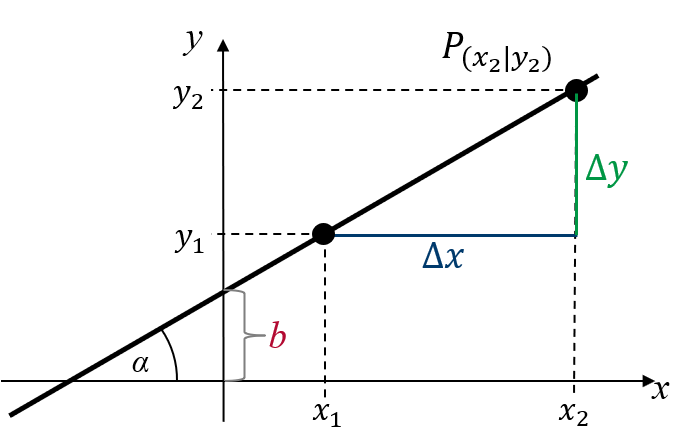 Die Normalform einer Geraden lautet:
Die Normalform einer Geraden lautet:$ f(x) = y = \color{blue}{m}x + \color{red}{b} $
$ \color{blue}{m} $: Steigung der Geraden mit $ m = \frac{\color{green}{\Delta y}}{\color{darkblue}{\Delta x}} = \tan(\alpha) $
$ \color{red}{b} $: $y$-Achsenabschnitt
Für alle Punkte $ P(x_i|y_i) $, die auf einer Geraden liegen, gilt damit: $ y_i = mx_i + b $
Übrigens: Kennen Sie dieses Zeichen ? Wenn nicht, dann klicken Sie auf das Smiley.
🧐
Wir unterscheiden drei Fälle, je nach Wert der Steigung :
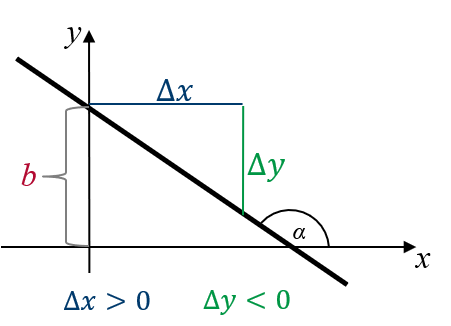
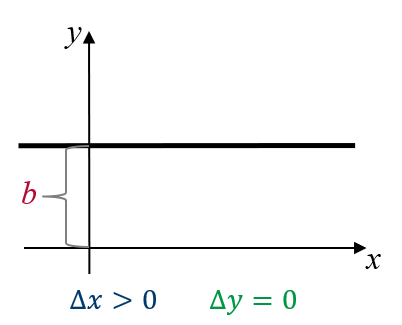
| $m > 0$ | $m < 0$ | $m = 0$ |
| Die Gerade ist streng monoton wachsend. | Die Gerade ist streng monoton fallend. | Die Gerade ist eine Konstante. |
| Für $x_1 < x_2$ ist $f(x_1) < f(x_2)$. | Für $x_1 < x_2$ ist $f(x_1) > f(x_2)$. | Für $x_1 < x_2$ ist $f(x_1) = f(x_2)$. |
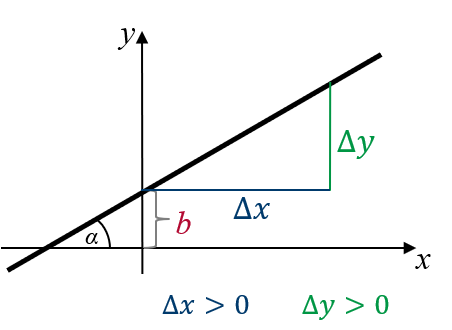 |  |  |
Lage zweier Geraden¶
Bezüglich der Lage zweier Geraden zueinander unterscheidet man drei Fälle:
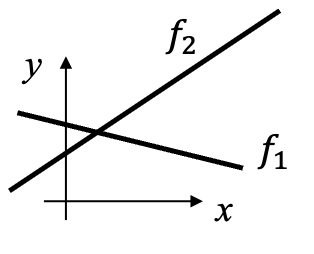
Zwei Geraden haben einen Schnittpunkt, falls ihre Steigungen $ m_1 $ und $ m_2 $ ungleich sind.
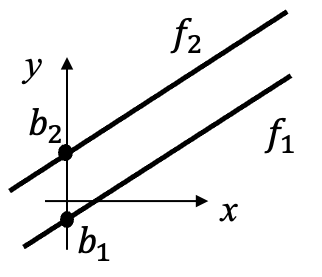
Zwei Geraden haben keinen Schnittpunkt bzw. sind parallel, falls ihre Steigungen $ m_1 $ und $ m_2 $ gleich und ihre $y$-Achsenabschnitte $ b_1$ und $b_2$ ungleich sind.
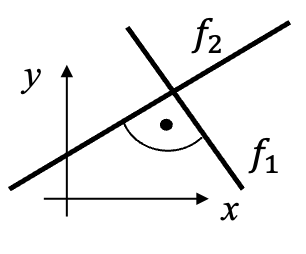
Zwei Geraden stehen senkrecht (orthogonal) aufeinander, falls das Produkt ihrer Steigungen $m_1$ und $ m_2$ gleich -1 ist.
Bestimmung der Geradengleichung¶
Eine Gerade ist eindeutig festgelegt durch die Angabe
zweier auf der Geraden liegender Punkte oder
eines auf der Geraden liegendes Punktes und der Steigung der Geraden.
Um die Geradengleichung zu bestimmen, können Sie in beiden Fällen die Normalform einer Geraden verwenden und die fehlenden Parameter durch Einsetzen der gegebenen Größen bestimmen. Wenn Ihnen das nicht klar ist, dann sehen Sie sich die im Folgenden gegebenen Beispiele an.
Gegeben: Zwei voneinander verschiedene Punkte auf der Geraden
🧐
Für beide Punkte $P_1$ und $P_2$ auf der Geraden muss die Geradengleichung $y_i = m\cdot x_i+b$ gelten. Wir setzen also die Koordinaten der beiden Punkte ein und erhalten:
$1 = m\cdot 1 + b$
$4 = m\cdot 3 + b$
Aus diesen beiden Gleichungen können nun die beiden unbekannten Parameter $m$ und $b$ bestimmt werden. Aus der ersten Gleichung erhalten wir z.B. $m=1-b$. Eingesetzt in die zweite Gleichung ergibt sich:
$4 = (1-b)\cdot 3 + b \quad\Leftrightarrow\quad 4 = 3 -3b +b \quad\Leftrightarrow\quad 1 = -2b \quad\Leftrightarrow\quad b = -\frac{1}{2}$
Damit erhalten wir für $m=1-b=1-\left(-\frac{1}{2}\right) = \frac{3}{2}$
Die Geradengleichung lautet damit: $y = \frac{3}{2}x-\frac{1}{2}$
🦉
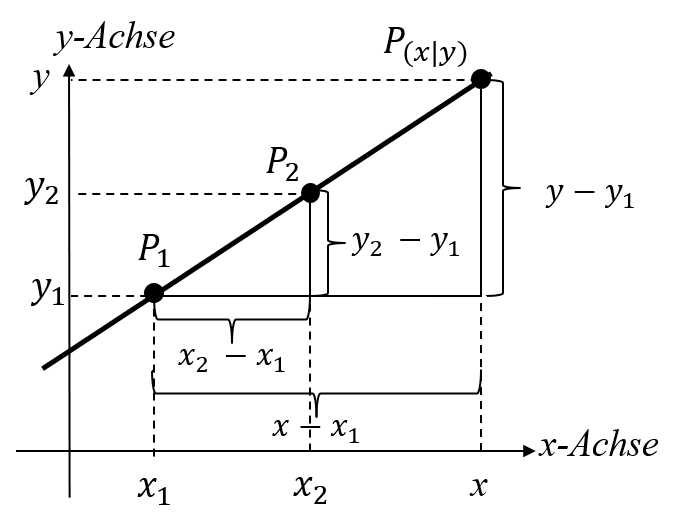 Sind die beiden voneinander verschiedenen Punkte $P_1(x_1|y_1)$ und $P_2(x_2|y_2)$ gegeben, so ergibt sich nach dem zweiten Strahlensatz für einen beliebigen Punkt $P(x|y)$ auf der Geraden die Gleichung (siehe Skizze rechts):
Sind die beiden voneinander verschiedenen Punkte $P_1(x_1|y_1)$ und $P_2(x_2|y_2)$ gegeben, so ergibt sich nach dem zweiten Strahlensatz für einen beliebigen Punkt $P(x|y)$ auf der Geraden die Gleichung (siehe Skizze rechts): $ \frac{y-y_1}{x-x_1} = \frac{y_2-y_1}{x_2-x_1} \qquad \Rightarrow \qquad $ Zwei-Punkte-Form
Einsetzen der Koordinaten der beiden gegebenen Punkte und anschließendes Auflösen der Gleichung nach $y$ liefert die Normalform der gesuchten Gerade.
Verwenden wir die beiden zuvor gegebenen Punkte $P_1$ und $P_2$ als Beispiel, so erhalten wir:
$ \frac{y-1}{x-1} = \frac{4-1}{3-1} \quad\Leftrightarrow\quad (y-1) = \frac{3}{2}(x-1) \quad\Leftrightarrow\quad (y-1) = \frac{3}{2}x - \frac{3}{2} \quad\Leftrightarrow\quad y = \frac{3}{2}x - \frac{1}{2}$
Bemerkung: Es ist vollkommen ausreichend, wenn Sie eine der beiden Berechnungsmöglichkeiten kennen. Wählen Sie einfach diejenige aus, die Ihnen leichter fällt.
Gegeben: Ein Punkt auf der Geraden und deren Steigung
🧐
Die Steigung $m$ kann direkt in die Normalform der Geradengleichung eingesetzt werden. Für alle Punkte, die auf der Geraden liegen, muss also die Geradengleichung $y_i = 2\cdot x_i+b$ gelten.
Setzen wir nun in einem zweiten Schritt noch die Koordinaten des gegebenen Punktes $P$ ein, ergibt sich:
$3 = 2\cdot 2 + b \quad\Leftrightarrow\quad b = -1$
Die Geradengleichung lautet damit: $y = 2x-1$
🦉
$m = \frac{\Delta y}{\Delta x} = \frac{y-y_1}{x-x_1}$, wobei $x$ und $y$ die Koordinaten eines beliebigen Punktes $P$ auf der Geraden sind.
Auch hier kann man die gegebenen Werte einsetzen und anschließend die Gleichung nach $y$ auflösen.
Verwenden wir die zuvor gegebenen Größen als Beispiel, so erhalten wir:
$ 2 = \frac{y-3}{x-2} \quad\Leftrightarrow\quad 2(x-2) = (y-3) \quad\Leftrightarrow\quad (y-3) = 2x - 4 \quad\Leftrightarrow\quad y = 2x-1$
Bemerkung: Auch hier genügt es, wenn Sie eine der beiden Berechnungsmöglichkeiten kennen. Wählen Sie diejenige aus, die Ihnen leichter fällt.
Aufgaben¶
Generieren Sie sich nun Aufgaben zum Üben. Die Schwierigkeit der Aufgabe kann über das in Klammern angegebene Level gewählt werden. Führen Sie die folgende Zelle aus, indem Sie zunächst in die Zelle klicken und dann Steuerung und Enter gleichzeitig drücken. Dadurch erhalten Sie die Aufgabe der Schwierigkeitsstufe 1. Berechnen Sie anschließend die Lösung der Aufgabe mit Stift und Papier und geben Sie das berechnete Ergebnis in das Textfeld ein. Durch Klicken auf den Button “Überprüfen” können Sie Ihr Ergebnis überprüfen. Wenn Sie nicht weiterkommen, dann klicken Sie auf die Glühbirne, um einen Tipp zu erhalten.
Teil A¶
# Generiere Aufgabe mit Schwierigkeitsstufe 1 durch gleichzeitiges Drücken von Steuerung und Enter
Funktionen.Lineare_Funktionen.Aufgabe(level=1)# Generiere Aufgabe mit Schwierigkeitsstufe 2 durch gleichzeitiges Drücken von Steuerung und Enter
Funktionen.Lineare_Funktionen.Aufgabe(level=2)Teil B¶
# Generiere Aufgabe mit Schwierigkeitsstufe 3 durch gleichzeitiges Drücken von Steuerung und Enter
Funktionen.Lineare_Funktionen.Aufgabe(level=3)