Skip to article frontmatterSkip to article content

Funktionen

Handwerkszeug für dieses Notebook:

Rechenoperationen:

Multiplikation:  *

Division und Brüche:  /

Eingabe von Potenzen:  **

Eingabe eines Kommas als Punkt:  .

Eine Zelle ausführen:  Enter und Shift gleichzeitig

Wurzeln: Quadratwurzeln: x= \sqrt{x} = sqrt(x) und n-te Wurzeln: xn= \sqrt[n]{x} = x**(1/n)

e e -Funktion: ex e^x = exp(x)

Logarithmen: ln(x) bzw. log(x)

Egal, wo Sie sich im Notebook befinden: Wenn Sie Fragen zur Eingabe haben, können Sie einfach eine Zelle generieren, dort Spickzettel() eintragen und die Zelle durch gleichzeitiges Drücken der Shift und der Enter-Taste ausführen. Daraufhin erscheint noch einmal eine Liste mit Hinweisen, wie was eingegeben werden muss. Probieren Sie das gerne gleich einmal aus, indem Sie die nächste Zelle auführen.
 

# Führen Sie diese Zelle aus. Damit erhalten Sie nochmal alle Hinweise zu den nötigen Eingaben
Spickzettel()

Wozu braucht man Funktionen?

Grundsätzlich ordnet eine Funktion einer Zahl genau eine andere Zahl zu.

Keine Naturwissenschaft kommt ohne Funktionen aus:

In der Biologie wird das Wachstum von Bakterienkulturen durch Funktionen ausgedrückt, in der Physik sind die Geschwindigkeits-Zeit-Gesetze ein Beispiel, in der Chemie beschreiben Wellenfunktionen den quantenmechanischen Zustand von Elementarteilchen...

Aber auch im Alltag haben wir ständig mit Funktionen zu tun: Zuordnungen von Preisen von Produkten, Verschlüsselungsfunktionen verschlüsseln Geheimzahlen von Bankkarten und leiten sie an einen Server weiter, der Benzinverbrauch im Auto kann durch eine Funktion beschrieben werden...

Bild von Gerd Altmann auf Pixabay

Bewegen Sie sich in den nächsten Tagen mit offenen Augen durch Ihren Alltag: Wo könnte eine Funktion dahinter stecken?

In diesem und den folgenden Notebooks gibt es einen Überblick über das wichtige Thema Funktionen. Um die Länge der Notebooks überschaubar zu halten, sind die Erklärungen teilweise sehr knapp. Durch Klicken auf das Smiley mit Lupe 🧐 gibt es aber an vielen Stellen noch einmal eine genauere Erklärung der Sachverhalte.

Definition von Funktionen

Eine reellwertige Funktion einer reellen Veränderlichen ist eine Vorschrift $f$, die jeder Zahl $x \in D \subseteq \mathbb{R} $ genau eine Zahl $ f(x) \in W \subseteq \mathbb{R}$ zuordnet.

In dieser Definition werden die mathematische Symbole R\mathbb{R}, ∈\in und ⊆\subseteq verwendet. Wenn Ihnen die Bedeutungen dieser Symbole nicht mehr geläufig sind, dann klicken Sie auf das Smiley. Alle weiteren in der Definition verwendeten Bezeichnungen werden in den folgenden beiden Kästen erklärt.

🧐
$\mathbb{R}$: Menge der reellen Zahlen
Die beiden anderen Symbole kommen aus der Mengenlehre. Sie bedeuten in Worten:

  • $\in$: ist Element von (also als Beipsiel: $x \in D$ heißt "$x$ ist ein Element der Menge $D$")

  • $\subseteq$: ist Teilmenge von (als Beispiel: $D \subseteq \mathbb{R}$ heißt "$D$ ist Teilmenge der reellen Zahlen")

$ \color{red}{x}$ heißt unabhängige Variable oder Argument von $f$.

f(x) \color{green}{f} \color{black}{(} \color{red}{x} \color{black}{)} heißt Funktionswert von f \color{green}{f} an der Stelle x\color{red}{x}.

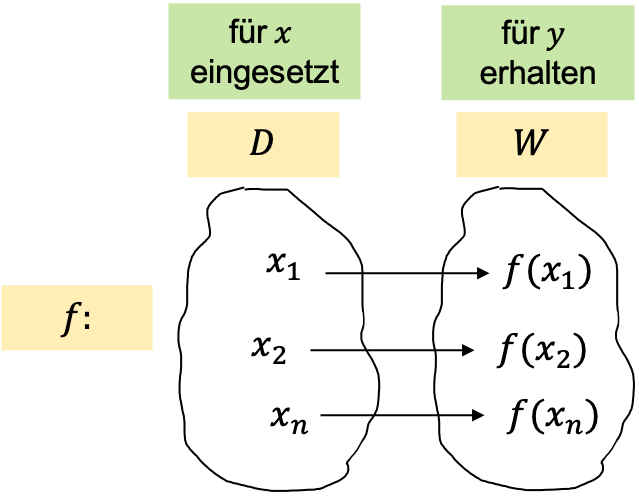Definitions- und Wertemenge:

D⊆R D \subseteq \mathbb{R} Definitionsmenge: Teilmenge der reellen Zahlen, an denen die Funktion ausgewertet werden darf

W⊆R W \subseteq \mathbb{R} Wertemenge: Menge der Funktionswerte

🧐
Aber wie bestimme ich eigentlich Definitions- und Wertebereich einer Funktion?
Zur Bestimmung des Definitionsbereichs ist folgende Frage hilfreich: Bei welchen $x$-Werten versagt die Funktion bzw. welche $x$-Werte darf man nicht in die Funktionsvorschrift einsetzen (siehe dazu auch Beispiel 3 im Folgenden). Diese $x$-Werte dürfen dann nicht im Definitionsbereich der Funktion enthalten sein.
Um den Wertebereich einer Funktion zu bestimmen, ist folgende Frage nützlich: Welche $y$-Werte werden von der Funktion erzeugt und welche nicht? Alle Werte, die von der Funktion erzeugt werden können, bilden den Wertebereich.
Probieren Sie diese Fragen an den folgenden Beispielen einfach einmal aus.

Beispiele:

  1.   f(x)=x2f(x) = x^2 :    x∈D=R x \in D = \mathbb{R},    W=[0,∞) W = [0, ∞)
🧐
In $f(x) = x^2$ kann man für $x$ jede beliebige reelle Zahl einsetzen. Daraus ergibt sich als Definitionsbereich also die Menge der reellen Zahlen. Die Funktionswerte, die man erhält, sind aufgrund des Quadrates entweder null oder positiv, wodurch sich der angegebene Wertebereich ergibt.
  1. Kugelvolumen  V(r)=43πr3 V(r) = \frac{4}{3} \pi r^3 :     D=[0,∞) D = [0, ∞) ,     W=[0,∞) W = [0, ∞)
🧐
Da es sich hier um die Berechnungsformel für das Volumen einer Kugel handelt, ist es sinnvoll, für den Radius $r$ nur positive reelle Zahlen und null zuzulassen. Dadurch erklärt sich der hier angegebene Definitionsbereich. Der Wertebereich umfasst dann ebenfalls nur positive reelle Zahlen einschließlich der Null.
  1.   f(x)=1x f(x) = \frac{1}{x} :     D=R∖{0} D = \mathbb{R} \setminus{\{0\}} ,     W=R∖{0} W = \mathbb{R} \setminus{\{0\}}
🧐
Diese Funktion ist für $x$=0 nicht definiert, da man durch Null nicht teilen darf. Alle anderen reellen Zahlen können aber eingesetzt werden. Daher umfasst der Definitionsbereich alle reellen Zahlen außer Null. Das Ausschließen von Elementen aus der Menge der reellen Zahlen kann wie oben dargestellt über einen Backslash geschrieben werden. Die in den geschweiften Klammern aufgeführten Elemente (hier die Null) sind die Elemente, die aus der zuvor genannten Menge ausgeschlossen werden. Als Funktionswerte können dann ebenfalls alle reelle Zahlen außer Null auftreten.

Eine alternative Schreibweise für die Angabe des Definitions- und Wertebereiches einer Funktion ist folgende: f:D→Wf: D \to W
Beispiel 1 würde man damit schreiben als:
f:R→[0,∞)f: \mathbb{R} \to [0, \infty)
      f(x)=x2f(x)=x^2

Funktionsgraphen: Darstellung von Funktionen

Der Graph $G$ einer Funktion ist die Punktemenge $ G:=\left\{\left(x|f(x)\right): x \in D, f(x) \in W\right\}$
🧐
In dieser Definition stehen einige mathematische Kurzschreibweisen, die vielleicht noch nicht jeder kennt. Daher ist hier noch einmal die Definition aufgeführt. Darunter steht in Worten die Bedeutung der einzelnen Teile. Die Menge $D$ entspricht wieder der Definitionsmenge und die Menge $W$ der Wertemenge.

Beispiel:

f(x)=11+x2 f(x) = \frac{1}{1 + x^2}

Überlegen Sie zunächst kurz, wie der Funktionsgraph dieser Funktion aussieht.

Funktionsgraphen von Hand zu erstellen kann (je nach angestrebter Genauigkeit) sehr mühsam sein. Daher wollen wir uns an dieser Stelle den Computer zu nutze machen und die gegebene Funktion mit SymPy darstellen. SymPy ist eine Python-Bibliothek, die verschiedene Funktionen für symbolische mathematische Berechnungen bereit stellt. Sie kann also mit Variablen (wie z.B. xx) rechnen. Um die Funktionen aus der Bibliothek verwenden zu können, müssen diese zunächst importiert werden. Dies wollen wir in der folgenden Code-Zelle machen. Alles, was hinter dem “#”-Symbol steht, wird nicht vom Computer interpretiert. Es handelt sich dabei um Kommentartexte. Schauen Sie sich nun zunächst den Code mit den Kommentaren an und führen Sie die Zelle dann aus.

from sympy import* # Import der gesamten SymPy-Bibliothek, so dass alle Funktionen in diesem Notebook zur Verfügung stehen
from sympy.plotting import plot # Import der Funktion 'plot' aus der Bibliothek sympy.plotting.

# Hinweis: Der Import der SymPy-Bibliothek und der Funktion 'plot' muss nur einmal erfolgen und steht 
#          dann (nach Auführung der Zelle) im gesamten Notebook zur Verfügung.
#
# Führen Sie diese Zelle nun durch gleichzeitiges Drücken von Shift (Umschalttaste) und Enter (Eingabetaste) aus

Wir benötigen nun noch zwei Code-Zeilen (siehe folgende Code-Zelle), um den Graphen der Funktion f(x)f(x) zu erhalten. Sehen Sie sich auch diese Zelle an und führen Sie sie am Ende aus.

# Wir definieren zunächst x als SymPy-Symbol und sagen damit dem Computer, dass im Folgenden x als Variable in Ausdrücken 
# auftreten darf.
x = symbols('x')

# Nun können wir die plot-Funktion verwenden, um den Graphen darzustellen. Dazu schreiben wir den Befehl 'plot' und dahinter in Klammern die Funktion, 
# die wir darstellen wollen.
plot(1/(1+x**2))

# Führen Sie nun diese Zelle aus, um den Graphen der Funktion zu sehen.

Betrachten Sie die Funktion und überlegen Sie, welchen Definitions- und welchen Wertebereich die Funktion hat. Auf der Glühbirne erhalten Sie weitere Informationen dazu. Durch Klicken auf den Stift erhalten Sie die Lösung.

💡
Definitionsbereich: Welche Zahlen dürfen für $x$ eingesetzt werden?

Wertebereich: In welchem Bereich liegen die Funktionswerte f(x)f(x)?

✏️
Für $x$ dürfen alle reellen Zahlen eingesetzt werden. Der Definitionsbereich ist damit: $ D_f = \mathbb{R} $

Die Funktionswerte liegen zwischen 0 und 1, wobei die 0 nie ganz erreicht wird. Der Wertebereich ist folglich: W_f = (0,1]

Eine Funktion ist nur dann eine Funktion, wenn jeder Zahl $x \in D $ genau eine Zahl zugeordnet wird.
# Führen Sie diese Zelle aus, um einen Beispielgraphen zu sehen, der KEINE Funktion darstellt
Demo.Darstellung_Beispielgraph()

Die senkrechte rote Linie verdeutlicht, dass dem Wert xx aus dem Definitionsbereich an dieser Stelle zwei Werte zugeordnet werden können. Dies widerspricht der Definition einer Funktion!

Aufgaben

Generieren Sie sich nun Aufgaben zum Üben. Die Schwierigkeit der Aufgabe kann über das in Klammern angegebene Level gewählt werden. Führen Sie die folgende Zelle aus, indem Sie zunächst in die Zelle klicken und dann Steuerung und Enter gleichzeitig drücken. Dadurch erhalten Sie die Aufgabe der Schwierigkeitsstufe 1. Berechnen Sie anschließend die Lösung der Aufgabe mit Stift und Papier und geben Sie das berechnete Ergebnis in das Textfeld ein. Durch Klicken auf den Button “Überprüfen” können Sie Ihr Ergebnis überprüfen. Wenn Sie nicht weiterkommen, dann klicken Sie auf die Glühbirne, um einen Tipp zu erhalten.

Teil A
# Generiere Aufgabe durch gleichzeitiges Drücken von Steuerung und Enter
Demo.Funktionsgraph()
# Generiere Aufgabe durch gleichzeitiges Drücken von Steuerung und Enter
Funktionen.Funktionsgraph.Aufgabe(level=1)

Bestimmung des Funktionswertes

Die Variable xx kann als Platzhalter aufgefasst werden. Der Funktionswert an einer beliebigen Stelle xx aus dem Definitionsbereich kann dann durch Einsetzen des Wertes für xx ermittelt werden. Alternativ kann der Funktionswert auch graphisch aus dem Schaubild der Funktion bestimmt werden. Die Bestimmung aus dem Graphen der Funktion ist aber meistens sehr ungenau.

Beispiel:
Gegeben ist die Funktion f(x)=x2+2x+3f(x)=x^2+2x+3. Bestimmen Sie den Funktionswert an den Stellen x=5x=5 und x=t+3x=t+3.

Zur Bestimmung des Funktionswertes an der Stelle xx=5 können wir wie folgt vorgehen:

  1. Wir setzen an jeder Stelle, an der

    x

    in der Funktionsgleichung steht, die Zahl 5 ein. Damit erhalten wir:


    f(5)=5^2+2\cdot 5+3

  2. Nun können wir den Funktionswert weiter ausrechnen und erhalten:


    f(5)=25+10+3=38

Versuchen Sie nun analog dazu, den Funktionswert an der Stelle x=t+3 zu bestimmen. Durch Klicken auf den Stift erhalten Sie die Lösung.

✏️

Zur Bestimmung des Funktionswertes an der Stelle x=t+3 gehen wir analog vor:

  1. Für

    x

    setzen wir nun den Term

    t+3

    ein. Hierbei empfiehlt es sich, zunächst überall Klammern zu setzen, um z.B. keine Vorzeichenfehler zu generieren. Wir erhalten:


    f(t+3)=(t+3)^2+2\cdot (t+3)+3

  2. Wir rechnen nun wieder Schritt für Schritt die rechte Seite aus, um den Funktionswert

    f(t+3)

    zu erhalten. Dabei muss man vor allem auf eventuell auftretende Binomische Formeln und korrektes Ausmultiplizieren achten.


    f(t+3)=(t^2+6t+9)+2t+6+3=t^2+8t+18

Aufgaben

Generieren Sie sich nun nochmal Aufgaben zum Üben. Die Schwierigkeit der Aufgabe kann über das in Klammern angegebene Level gewählt werden. Führen Sie die folgende Zelle aus, indem Sie zunächst in die Zelle klicken und dann Steuerung und Enter gleichzeitig drücken. Dadurch erhalten Sie die Aufgabe der Schwierigkeitsstufe 1. Berechnen Sie anschließend die Lösung der Aufgabe mit Stift und Papier und geben Sie das berechnete Ergebnis in das Textfeld ein. Durch Klicken auf den Button “Überprüfen” können Sie Ihr Ergebnis überprüfen. Wenn Sie nicht weiterkommen, dann klicken Sie auf die Glühbirne, um einen Tipp zu erhalten.

Teil A
# Generiere Aufgabe mit Schwierigkeitsstufe 1 durch gleichzeitiges Drücken von Steuerung und Enter
Funktionen.Funktionswerte.Aufgabe(level=1)
# Generiere Aufgabe mit Schwierigkeitsstufe 2 durch gleichzeitiges Drücken von Steuerung und Enter
Funktionen.Funktionswerte.Aufgabe(level=2)
# Generiere Aufgabe mit Schwierigkeitsstufe 3 durch gleichzeitiges Drücken von Steuerung und Enter
Funktionen.Funktionswerte.Aufgabe(level=3)
Teil B
# Generiere Aufgabe mit Schwierigkeitsstufe 4 durch gleichzeitiges Drücken von Steuerung und Enter
Funktionen.Funktionswerte.Aufgabe(level=4)
Dreisatz Und Prozentrechnung
Prozentrechnung
Funktionen
Lineare Funktionen