Integralrechnung¶

Flächeninhalt und Stammfunktion¶

In diesem Notebook schauen wir uns die Bedeutung und den Zusammenhang von Stammfunktion, Flächeninhalt und Integral genauer an.

Zunächst stellen wir den Zusammenhang zwischen Funktion, Ableitung und Stammfunktion her.

Zusammenhang zwischen $ f(x), f'(x)$ und $ F(x) $:¶

Das Schema zeigt, wie Ableitung $f'(x)$, die Funktion $f(x)$ und die Stammfunktion $F(x)$ durch Ableiten und Integrieren zusammenhängen.

Zur Veranschaulichung betrachten wir die Funktion $f(x) = x^2+3x-3$

Betrachten Sie den Graphen der Funktion:
Der Graph der Funktion $f$ schneidet die $x$-Achse zweimal, besitzt also zwei Nullstellen. Außerdem hat er ein Minimum an der Stelle $x = - \frac{3}{2}$.

Nun betrachten wir die Ableitung $f'(x)$ und deren Graphen.

Oben wurde sichtbar, dass die Funktion $f$ an der Stelle $x = - \frac{3}{2}$ ein Minimum aufweist. Dort ist die Steigung der Tangente an den Graphen 0. Somit hat die Ableitungsfunktion an der Stelle eine Nullstelle. Der Graph der Ableitungsfunktion schneidet hier die $x$-Achse. Dies ist im zweiten Plot sichtbar.

Nun betrachten wir noch den Graphen einer Stammfunktion $F$ zur Funktion $f$.
Da die Funktion $f$ zwei Nullstellen besitzt, erwarten wir zwei Extremstellen für die Stammfunktion $F$.

Die Extremstelle des Graphen von $F$ im negativen Bereich ist ein Maximum. Die Steigung des Graphen von $F$ weiter links davon ist positiv, rechts davon negativ. Da die Funktion $f$ die Ableitung von $F$ darstellt, verläuft der Graph von $f$ hier oberhalb der $x$-Achse, danach unterhalb der $x$-Achse. Überlegen Sie sich diesen Zusammenhang für die zweite Extremstelle von $F$, dem Minimum.

Wenn Sie die folgende Zelle ausführen, erhalten Sie nochmals alle drei Graphen in einem Koordinatensystem.
Die Funktion $\color{blue}{f(x)}$ ist in Blau dargestellt,
Die Funktion $\color{orange}{f'(x)}$ ist in Orange dargestellt,
Die Funktion $\color{green}{F(x)}$ ist in Grün dargestellt.

Den Zusammenhang zwischen Funktion $f(x)$, Ableitung $f'(x)$ und der Stammfunktion $F(X)$ zu kennen und auch im Graphen der jeweiligen Funktionen zu verstehen ist extrem wichtig. Üben Sie dies nochmals anhand der folgenden Demo.

Deutung der Stammfunktion¶

Wir betrachten eine stückweise konstante Funktion $f(x)$.

Der Graph der Funktion $f$ ist in dunkelblau dargestellt. Er verläuft teilweise oberhalb, teilweise unterhalb und in einem Abschnitt auch auf der $x$-Achse.

Nun betrachten wir nur das Intevall $[a,b]$ und $F$ zu $f$.

Hat die Funktion $f$ negative Funktionswerte, so ist die Konstruktion des Integrals ebenfalls anwendbar. Dieses hat dann jedoch negative Werte.
Soll der Flächeninhalt der Fläche bestimmt werden, die der Graph von $f$ innerhalb des Intervalls $[a,b]$ mit der $x$-Achse einschließt, so muss dieser aus drei Teilen aufsummiert werden.

Rechnerisch kann ein bestimmtes Integral Null werden, obwohl die Funktion nicht die Nullfunktion ist und damit der Flächeninhalt betragsmäßig $> 0$ ist.

Beispiel:

Gesucht ist der Flächeninhalt, den der Graph der Funktion $f(x) = sin(x)$ mit der $x$-Achse einschließt.
$\int_{0}^{2\pi} \sin(x)$ $dx$ $= [-\cos(x)]_0^{2\pi}$
$= -\cos(2\pi) + \cos(0)$
$=-1 +1 =0$ $\color{red}{??}$

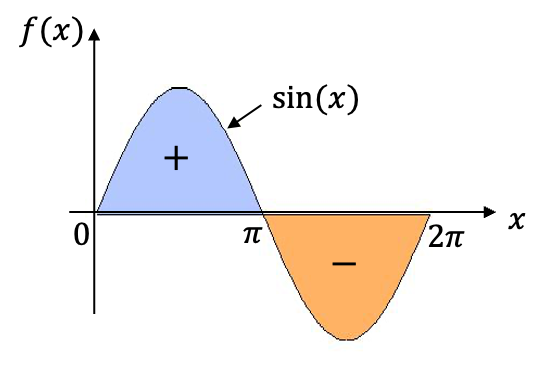
Im Bild wird deutlich, dass der Flächeninhalt jedoch $>0$ ist.

Rechenansatz für solche Fälle:

Für das hier aufgezeigte Beispiel mit den Nullstellen $x_1 = 0$; $x_2=\pi$ und $x_3 = 2\pi$ gilt dann:

$\vert \int_0^{\pi} \sin(x)$ $dx$ $\vert$ $+ \vert \int_{\pi}^{2\pi} \sin(x)$ $dx$ $\vert$
$= \vert [-\cos(x)]_0^{\pi} \vert + \vert [-\cos(x)]_{\pi}^{2\pi} \vert$
$= \vert - \cos(\pi) + \cos(0) \vert + \vert -\cos(2\pi) + \cos (\pi) \vert$
$= \vert - (-1) + 1 \vert + \vert -1 + (-1) \vert$
$= \vert 1 + 1 \vert + \vert -1 -1 \vert$
$= 2 +2 =4$

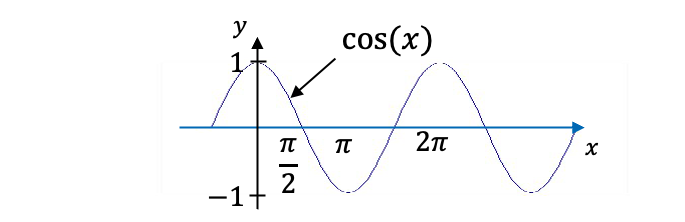
Zum Nachvollziehen der Werte der Cosinus-Funktion in der Rechnung ist diese hier nochmals abgebildet.

Aufgaben¶

Generieren Sie sich nun wieder Aufgaben zum Üben mit verschiedenen Schwierigkeitsstufen, die als Level jeweils in der Klammer angegeben sind. Führen Sie die folgenden Code-Zellen aus, indem Sie jeweils in die Zellen klicken und gleichzeitig Shift und Enter drücken. Bearbeiten Sie dann die Aufgaben, indem Sie sich Notizen mit Stift und Papier machen. Tippen Sie anschließend Ihr Ergebnis zur Überprüfung ein.

Teil A¶

Teil B¶