Integralrechnung¶

Eigenschaften bestimmter Integrale¶

Bestimmte Integrale haben Eigenschaften, die das Rechnen damit deutlich vereinfachen.

Ein beliebiger Faktor $k \in \mathbb{R}$ darf vor das Integral gezogen werden.

Beispiel:
$\int\limits_{2}^{3}$ $\color{red}{3}$ $x^2$ $dx$ $= \color{red}{3}$ $\int\limits_{2}^{3} x^2$ $dx$ $= 3 \cdot [ \frac{1}{3} x^3]_{2}^{3}$ $= 3 \cdot (\frac{1}{3} 3^3 - \frac{1}{3} 2^3) = 3 \cdot (\frac{27}{3} - \frac{8}{3}) = 3 \cdot \frac{19}{3} = 19$

Durch Vertauschen der Integrationsgrenzen ändert das Integral sein Vorzeichen.

Beispiel:
$\int\limits_{2}^{3}$ ${3}$ $x^2$ $dx$ $= [x^3]_{2}^{3}$ $= 3^3 - 2^3 = 19$

$\int\limits_{\color{red}{3}}^{2}$ ${3}$ $x^2$ $dx$ $= [x^3]_{\color{red}{3}}^{2}$ $= 2^3 - 3^3 = {\color{red}{-}}19$

Ein Integral kann in zwei oder mehr Teile geteilt werden. Dies hat keine Auswirkungen auf das Ergebnis. Die Fläche, die der Graph von $f$ mit der $x$-Achse einschließt, bleibt diesselbe.

Beispiel:
Wir nehmen das Rechenbeispiel von oben:
$\int\limits_{2}^{3}$ ${3}$ $x^2$ $dx$ $= [x^3]_{2}^{3}$ $= 3^3 - 2^3 = 19$
Hier können wir das Integral in zwei kleinere Teile teilen:

$\int\limits_{2}^{\frac{5}{2}}$ ${3}$ $x^2$ $dx$ $= [x^3]_{2}^{\frac{5}{2}}$ $= (\frac{5}{2})^3 - 2^3$
und
$\int\limits_{\frac{5}{2}}^{3}$ ${3}$ $x^2$ $dx$ $= [x^3]_{\frac{5}{2}}^{3}$ $= 3^3 - (\frac{5}{2})^3$

Nun werden die beiden Teile addiert:
$\int\limits_{2}^{\frac{5}{2}}$ ${3}$ $x^2$ $dx$ $+$ $\int\limits_{\frac{5}{2}}^{3}$ ${3}$ $x^2$ $dx$ $= (\frac{5}{2})^3 - 2^3 + 3^3 - (\frac{5}{2})^3$ $= 3^3 - 2^3 = 19$

Anwendung der dritten Eigenschaft:¶

Damit gilt auch: $\int\limits_{-\infty}^{+\infty} f(x)$ $dx$ $= \int\limits_{-\infty}^{0} f(x)$ $dx$ $+ \int\limits_{0}^{+\infty} f(x)$

Hieraus ergibt sich eine weitere wichtige Eigenschaft:
Wird von $-\infty$ bis $+\infty$ integriert, dann ist der Integrationsbereich um 0 symmetrisch. Einen um 0 symmetrischen Integrationsbereich erhält man in vielen Fällen. Hier sind weitere Beispiele aufgezeigt:
$\int\limits_{-3}^{+3} f(x)$ $dx$

$\int\limits_{-1}^{+1} f(x)$ $dx$

$\int\limits_{-273}^{+273} f(x)$ $dx$

Ist die untere Grenze gleich dem negativen Wert der oberen Grenze, dann ist der Integrationsbereich um 0 symmetrisch.

Betrachtung von geraden und ungeraden Funktionen über einen um 0 symmetrischen Integrationsbereich:

Ungerade Funktionen:

Das kann man sich anhand des Graphen einer ungeraden Funktion überlegen:

Zur besseren Veranschaulichung überlegen wir uns, wie groß die Fläche ist, die der Graph von $f(x) = x^3$ mit der $x$-Achse über einen um 0 symmetrischen Integrationsbereich einschließt. Wir verwenden den Bereich -7,5 bis 7,5.

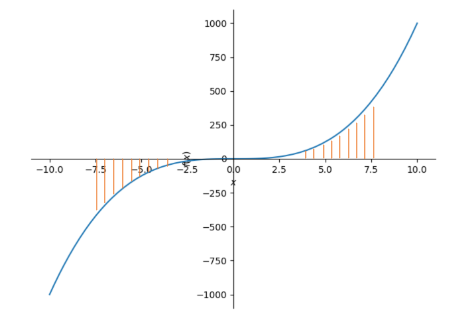
Die beiden orange schraffierten Teile sind vom Betrag her gleich groß, haben aber unterschiedliche Vorzeichen. Addiert man die beiden Teile bzw. die Integrale
$\int\limits_{-7,5}^{0} x^3$ $dx$
und
$\int\limits_{0}^{7,5} x^3$ $dx$
erhält man 0.

Zum weiteren Verständnis, warum ein bestimmtes Integral 0 werden kann, obwohl der Flächeninhalt betragsmäßig $>0$ ist, beachten Sie das folgende Notebook 05_Flaecheninhalt_und_Stammfunktion.ipynb

Gerade Funktionen:
$\int\limits_{-\infty}^{+\infty} f(x)$ $dx$ $= 2 \cdot$ $\int\limits_{-\infty}^{0} f(x)$ $dx$ $= 2 \cdot \int\limits_{0}^{+\infty} f(x)$ $dx$; $f(x)$ gerade

Das kann man sich anhand des Graphen einer geraden Funktion überlegen:

Zur besseren Veranschaulichung überlegen wir uns, wie groß die Fläche ist, die der Graph von $f(x) = x^2$ mit der $x$-Achse über einen um 0 symmetrischen Integrationsbereich einschließt. Wir verwenden den Bereich -7,5 bis 7,5.

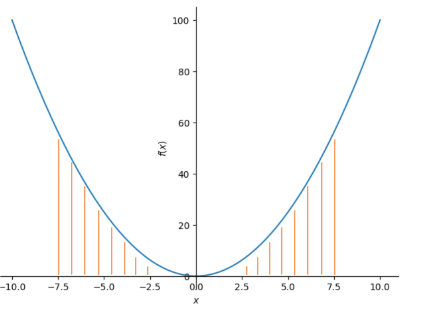
Die beiden orange schraffierten Teile sind vom Betrag her gleich groß. Da sie beide oberhalb der $x$-Achse liegen, haben beide Teile ein positives Vorzeichen. Addiert man die beiden Teile bzw. deren Integrale, erhält man als Ergebnis zweimal den linken Teil bzw. zweimal den rechten Teil.
$\int\limits_{-7,5}^{+7,5} x^2$ $dx$ $= 2 \cdot$ $\int\limits_{-7,5}^{0} x^2$ $dx$ $= 2 \cdot \int\limits_{0}^{+7,5} x^2$ $dx$
da:
$\int\limits_{-7,5}^{0} x^2$ $dx$ $= \int\limits_{0}^{+7,5} x^2$ $dx$

Ein Integral, bei dem die obere und die untere Integrationsgrenze gleich sind, ist gleich 0.

Beispiel:
$\int\limits_{2}^{2} 3 x^2$ $dx$ $= [3 \cdot \frac{1}{3} x^3]_{2}^{2} = 2^3 -2^3 = 0$

Das Integral über die Addition zweier Funktionen $f$ und $g$ kann auch als zwei einzelne Integrale geschrieben werden.

Beispiel:
$\int\limits_{2}^{3} x^2$ $dx$ $+ \int\limits_{2}^{3} {\color{green}{x}}$ $dx$ $= [ \frac{1}{3} x^3 ]_{2}^{3} + {\color{green}{[ \frac{1}{2} x^2 ]_{2}^{3}}}$ $= ( \frac{1}{3} \cdot (3^3-2^3)) + {\color{green}{(\frac{1}{2} \cdot (3^2 - 2^2))}}$ $= \frac{19}{3} + \frac{5}{2}$ $= \frac{53}{6}$ $= [ \frac{1}{3} x^3 + {\color{green}{\frac{1}{2} x^2}} ]_{2}^{3}$ $= \int\limits_{2}^{3} (x^2 + {\color{green}{x}})$ $dx$

Beispiel zur Anwendung mehrerer Eigenschaften in Kombination:

$\int\limits_{-1}^{1} (3 \cdot x^2 - x + 5)$ $dx$
$= \int\limits_{-1}^{1} (3 \cdot x^2)$ $dx$ $+ \int\limits_{-1}^{1} (-x)$ $dx$ $+ \int\limits_{-1}^{1} 5$ $dx$      s. 5. Eigenschaft
$= 3 \cdot \int\limits_{-1}^{1} x^2$ $dx$ $- \int\limits_{-1}^{1} x$ $dx$ $+ 5 \cdot \int\limits_{-1}^{1} 1$ $dx$      s. 1. Eigenschaft
$= 3 \cdot [\frac{1}{3} x^3]_{-1}^{1}$ $- [\frac{1}{2} x^2]_{-1}^{1}$ $+ 5 \cdot [x]_{-1}^{1}$
$= 3 \cdot [ \frac{1}{3} \cdot (1^3 - (-1)^3) ]$ $- [\frac{1}{2} \cdot (1^2 - (-1)^2)]$ $+ 5 \cdot [1- (-1)]$
$= 3 \cdot \frac{1}{3} \cdot 2 - 0 + 5 \cdot 2$
$= 2 + 10$
$= 12$

Aufgaben¶

Generieren Sie sich nun wieder Aufgaben zum Üben mit verschiedenen Schwierigkeitsstufen, die als Level jeweils in der Klammer angegeben sind. Führen Sie die folgenden Code-Zellen aus, indem Sie jeweils in die Zellen klicken und gleichzeitig Shift und Enter drücken. Bearbeiten Sie dann die Aufgaben, indem Sie sich Notizen mit Stift und Papier machen. Tippen Sie anschließend Ihr Ergebnis zur Überprüfung ein.

Teil A¶

Teil B¶