Skip to article frontmatterSkip to article content

Integralrechnung

Handwerkszeug für dieses Notebook:

Rechenoperationen:

Multiplikation:  *

Division und Brüche:  /

Eingabe von Potenzen:  **

Eingabe eines Kommas als Punkt:  .

Eine Zelle ausführen:  Enter und Shift gleichzeitig

Wurzeln: Quadratwurzeln: \sqrt{x} = sqrt(x) und n-te Wurzeln: \sqrt[n]{x} = x**(1/n)

e -Funktion: e^x = exp(x)

Logarithmen: ln(x) bzw. log(x)

Egal, wo Sie sich im Notebook befinden: Wenn Sie Fragen zur Eingabe haben, können Sie einfach eine Zelle generieren, dort Spickzettel() eintragen und die Zelle durch gleichzeitiges Drücken der Shift und der Enter-Taste ausführen. Daraufhin erscheint noch einmal eine Liste mit Hinweisen, wie was eingegeben werden muss. Probieren Sie das gerne gleich einmal aus, indem Sie die nächste Zelle auführen.
Eine neue Zelle generieren Sie übrigens, indem Sie oben in der Symbolleiste auf das Plus-Zeichen klicken.

Bestimmte Integrale

Es sei f : [a,b] \rightarrow \mathbb{R} stetig. Dann besitzt f eine Stammfunktion F und es gilt:
\int\limits_{a}^{b} f(x) dx = [F(x)]_{a}^{b} = F(b) - F(a)

Bestimmte Integrale besitzen im Gegensatz zu unbestimmten Integralen Integrationsgrenzen.

Wir überlegen uns die Definition bzw. Berechnung von bestimmten Integralen anhand eines Schaubilds:

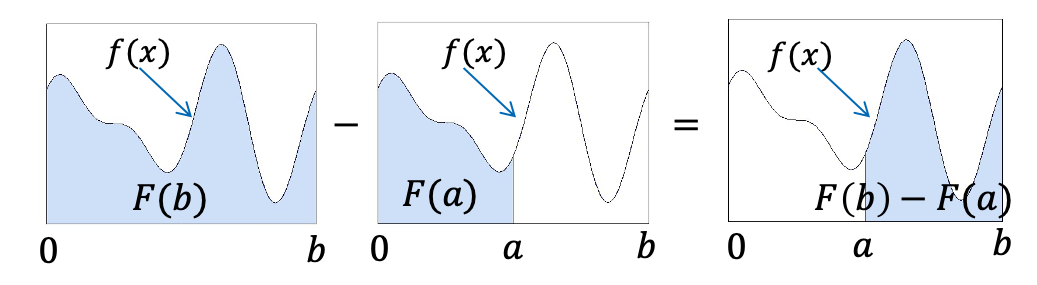
Mit bestimmten Integralen lassen sich anschaulich abgegrenzte Flächeninhalte bestimmen, die der Graph einer Funktion f(x)f(x) mit der xx-Achse in einem bestimmten Intervall einschließt.

Berechnung

  1. ∫−13x4 \int\limits_{-1}^{3} x^4 dxdx =[15x5]−13=(15⋅35−15⋅(−1)5)=15(243−(−1))=2445= [\frac{1}{5} x^5]_{-1}^{3} = (\frac{1}{5} \cdot 3^5 - \frac{1}{5} \cdot (-1)^5) = \frac{1}{5} (243- (-1)) = \frac{244}{5}
  1. ∫1e1x \int\limits_{1}^{e} \frac{1}{x} dxdx =[ln∣x∣]1e=ln∣e∣−ln∣1∣=1−0=1= [ln\vert x \vert]_{1}^{e} = ln \vert e \vert - ln \vert 1 \vert = 1-0 =1
  1. ∫01e−5t \int\limits_{0}^{1} e^{-5t} dxdx =[−15e−5t]01=−15(e−5⋅1−e−5⋅0)=−15(e−5t−1)=[- \frac{1}{5} e^{-5t}]_{0}^{1} = - \frac{1}{5} (e^{-5 \cdot 1} - e^{-5 \cdot 0}) = - \frac{1}{5} (e^{-5t} -1 )

Aufgaben

Generieren Sie sich nun wieder Aufgaben zum Üben mit verschiedenen Schwierigkeitsstufen, die in Leveln jeweils in der Klammer angegeben sind. Führen Sie die folgende Zelle aus, indem Sie in die Zelle klicken und gleichzeitig Shift und Enter drücken. Bearbeiten Sie dann die Aufgabe, indem Sie sich Notizen mit Stift und Papier machen und anschließend Ihr Ergebnis eintippen.

Teil A
#Generiere Aufgabe der Schwierigkeitsstufe 1 durch gleichzeitiges Drücken von Shift und Enter
Integralrechnung.Bestimmte_Integrale.Aufgabe(level=1)
#Generiere Aufgabe der Schwierigkeitsstufe 2 durch gleichzeitiges Drücken von Shift und Enter
Integralrechnung.Bestimmte_Integrale.Aufgabe(level=2)
#Generiere Aufgabe der Schwierigkeitsstufe 3 durch gleichzeitiges Drücken von Shift und Enter
Integralrechnung.Bestimmte_Integrale.Aufgabe(level=3)
#Generiere Aufgabe der Schwierigkeitsstufe 4 durch gleichzeitiges Drücken von Shift und Enter
Integralrechnung.Bestimmte_Integrale.Aufgabe(level=4)
#Generiere Aufgabe der Schwierigkeitsstufe 5 durch gleichzeitiges Drücken von Shift und Enter
Integralrechnung.Bestimmte_Integrale.Aufgabe(level=5)
#Generiere Aufgabe der Schwierigkeitsstufe 6 durch gleichzeitiges Drücken von Shift und Enter
Integralrechnung.Bestimmte_Integrale.Aufgabe(level=6)
Teil B
#Generiere Aufgabe der Schwierigkeitsstufe 7 durch gleichzeitiges Drücken von Shift und Enter
Integralrechnung.Bestimmte_Integrale.Aufgabe(level=7)
#Generiere Aufgabe der Schwierigkeitsstufe 8 durch gleichzeitiges Drücken von Shift und Enter
Integralrechnung.Bestimmte_Integrale.Aufgabe(level=8)
#Generiere Aufgabe der Schwierigkeitsstufe 9 durch gleichzeitiges Drücken von Shift und Enter
Integralrechnung.Bestimmte_Integrale.Aufgabe(level=9)
#Generiere Aufgabe der Schwierigkeitsstufe 10 durch gleichzeitiges Drücken von Shift und Enter
Integralrechnung.Bestimmte_Integrale.Aufgabe(level=10)
Integralrechnung
Unbestimmte Integrale
Integralrechnung
Eigenschaften Bestimmter Integrale