Integralrechnung¶
Handwerkszeug für dieses Notebook:¶
Rechenoperationen:
Multiplikation: *
Division und Brüche: /
Eingabe von Potenzen: **
Eingabe eines Kommas als Punkt: .
Eine Zelle ausführen: Enter und Shift gleichzeitig
Wurzeln: Quadratwurzeln: \sqrt{x} = sqrt(x) und n-te Wurzeln: \sqrt[n]{x} = x**(1/n)
e -Funktion: e^x = exp(x)
Logarithmen: ln(x) bzw. log(x)
Egal, wo Sie sich im Notebook befinden: Wenn Sie Fragen zur Eingabe haben, können Sie einfach eine Zelle generieren, dort Spickzettel() eintragen und die Zelle durch gleichzeitiges Drücken der Shift und der Enter-Taste ausführen. Daraufhin erscheint noch einmal eine Liste mit Hinweisen, wie was eingegeben werden muss. Probieren Sie das gerne gleich einmal aus, indem Sie die nächste Zelle auführen.
Eine neue Zelle generieren Sie übrigens, indem Sie oben in der Symbolleiste auf das Plus-Zeichen klicken.
Spickzettel()Definitionen¶
Es wird zwischen bestimmten und unbestimmten Integralen untschieden.
Bestimmtes Integral: Ordnet durch Integrationsgrenzen einer Funktion eine Zahl zu, die im zweidimensionalen Koordinatensystem dem Flächeninhalt zwischen Graph, -Achse und den Integrationsgrenzen entspricht.
Unbestimmtes Integral: Entspricht einer Menge von Stammfunktionen; die Ableitung dieser Stammfunktionen entspricht der ursprünglichen Funktion .
Schauen wir uns zuerst ein paar Begriffe an:
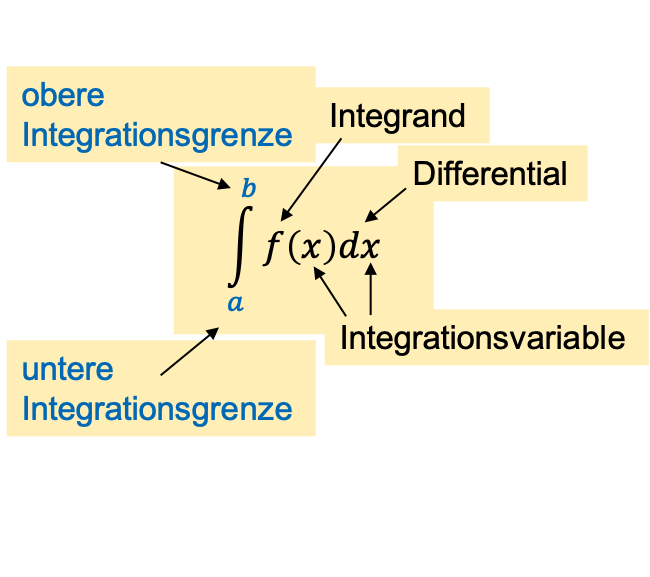
In der Grafik sind auch obere und untere Integrationsgrenze aufgezeigt. Diese sind nur bei bestimmten Integralen relevant.
Was steckt hinter der Berechnung eines Integrals?¶
Annäherung:
Die Fläche, die ein Graph einer Funktion mit der -Achse einschließt, soll bestimmt werden. Es geht also um die “Fläche unter der Kurve”. Dabei ist es schwierig, die Fläche einfach über eine Formel für ein zweidimensionales n-Eck zu bestimmen, da es sich nicht um ein n-Eck handelt. Deswegen geht man so vor, dass die zu bestimmende Fläche in kleine Flächeninhalte, also kleine Rechtecke, unterteilt wird. In der folgenden Grafik ist aufgezeigt, wie eine solche Aufteilung aussehen kann: Links sind die Rechtecke kleiner als die eigentliche Fläche, rechts sind sie größer. Man spricht bei der kleineren Fläche von der Untersumme, bei der größeren von der Obersumme.
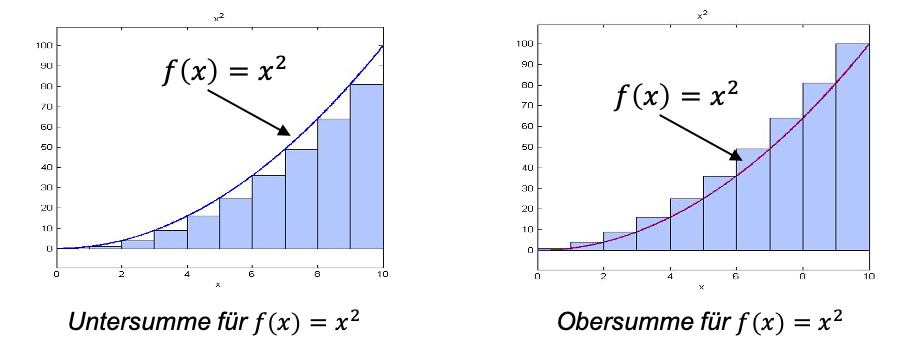
Die Untersumme ist kleiner als die gesuchte Fläche, die Obersumme dagegen größer, weswegen der Flächeninhalt so nur ungenau dargestellt werden kann.
Die Idee ist jetzt, dass das Intervall auf der -Achse verfeinert wird. Die Breite der Rechtecke wird also kleiner. Damit wird der Flächeninhalt eines jeden Rechtecks kleiner, die Anzahl der Rechtecke unter dem Graphen größer und die Summe der Flächeninhalte der Rechtecke nähert sich immer mehr dem tatsächlich gesuchten Flächeninhalt an.
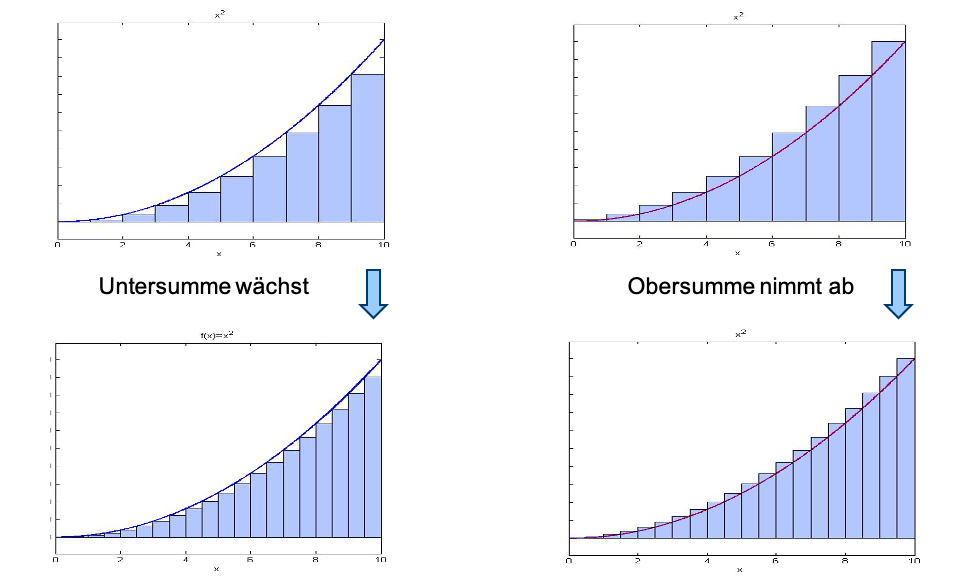
Nun lässt man die Anzahl der kleinen Flächeninhalte unendlich groß werden und bildet den Grenzwert der Summe. Das ergibt das bestimmte Integral.
Hierfür werden der Grenzwert und das Summenzeichen verwendet. Falls Sie mehr dazu erfahren möchten, klicken Sie auf den Smiley.
🧐
Die mathematische Notation einer Summe erfolgt mit dem Summenzeichen \sum.
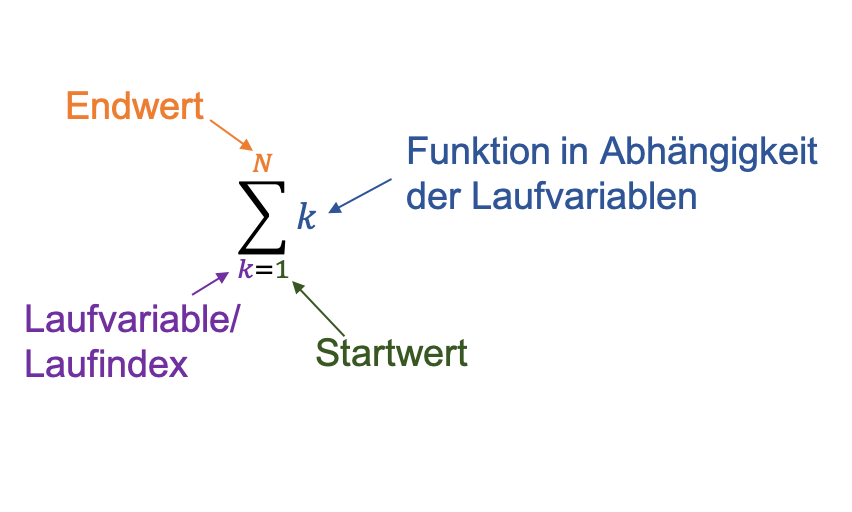
Es gilt zum Beispiel: 1 + 2 + 3 + 4 + 5 = \sum_{k=1}^5 k
Wie hier ersichtlich können die Laufvariable mit dem Startwert und der Endwert sowohl hinter der Summe als auch darunter und darüber stehen.
lim:
lim_{x\to\infty}f(x), gesprochen als “Limes f von x für x gegen unendlich”, stellt den Grenzwert einer Funktion f von x gegen unendlich dar.
Am Beispiel des Grenzwerts einer Summe hätten wir Folgendes:
lim_{N\to\infty}\sum_{k=1}^N : “Limes der Summe k=1 bis N für N gegen unendlich.” Hier wird der Grenzwert einer Summe gebildet.
Wir schauen uns an, was in den einzelnen Termen steht:
:
Hier wird die Anzahl der Flächeninhalte, die unterhalb des Graphen ansetzen, also die Untersumme, unendlich groß.
: Höhe der Rechtecke
: Breite der Rechtecke; diese ist definiert als die Differenz zweier aufeinander folgender -Werte
:
Hier wird die Anzahl der Flächeninhalte, die oberhalb des Graphen ansetzen, also die Obersumme, unendlich groß.
: Höhe der Rechtecke
: Breite der Rechtecke; diese ist definiert als die Differenz zweier aufeinander folgender -Werte.
:
bestimmtes Integral der Funktion mit den Integrationsgrenzen und
Die Begriffe “Ober- und Untersumme” und wie man diese berechnet werden im Video “Ober- und Untersumme” unter https://
Wenn jeder Flächeninhalt zwischen dem Graphen einer Funktion und der -Achse innerhalb zweier Grenzen mittels Ober- und Untersumme bestimmt werden müsste, wäre das sehr mühsam.
Deswegen wird der Zusammenhang zwischen Integral und Ableitung verwendet.
f sei eine auf dem offenen Intervall (c,b) definierte Funktion.
Jede differenzierbare Funktion F: (c,b) \rightarrow \mathbb{R} mit F' = \frac{dF}{dx} = f heißt Stammfunktion.
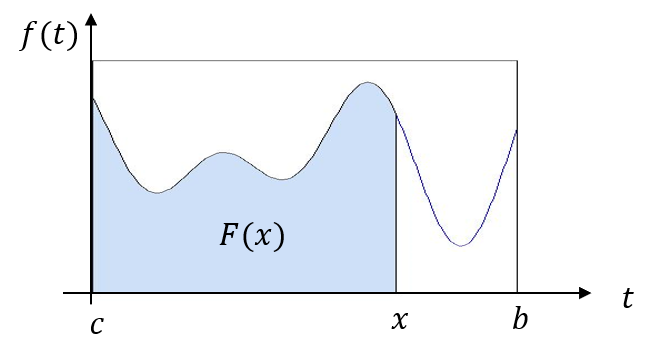
F(x):= \int_{c}^{x}f(t)dt
F(x) ist die Fläche unter dem Graphen von f zwischen t = c und t = x.
Beispiele:
Das heißt ist Stammfunktion von .
Das heißt ist Stammfunktion von
Das heißt ist Stammfunktion von .
Das heißt ist Stammfunktion von .
Wird die Stammfunktion abgeleitet, erhält man die Funktion . Ableitungen wurden im Kapitel Differentialrechnung bearbeitet. Die wichtigsten Ableitungsregeln gibt es im Ordner Differentialrechnung im Notebook: 02
In den folgenden Aufgaben haben Sie die Möglichkeit, nochmals Ableiten zu üben.
Aufgaben¶
Oben haben Sie gelernt, dass Sie durch das Ableiten der Stammfunktion wieder die Funktion erhalten. , und hängen also einerseits durch Ableiten zusammen, andererseits können Eigenschaften der Funktion mittels und bestimmt werden.
Erinnern Sie sich nochmals an das Thema Differentialrechnung und die grundlegenden Ableitungsregeln (02
Generieren Sie sich nun wieder Aufgaben zum Üben. Unten sind einige Aufgaben verschiedener Level zu verschiedenen Ableitungsregeln zusammengestellt. Wenn Sie Übungen zu weiteren Leveln bearbeiten wollen, ändern sie einfach die Zahl in der Klammer bei Level= .
Führen Sie die folgende Zelle aus, indem Sie in die Zelle klicken und gleichzeitig Shift und Enter drücken. Bearbeiten Sie dann die Aufgabe, indem Sie sich Notizen mit Stift und Papier machen und anschließend Ihr Ergebnis eintippen.
Teil A¶
#Generiere Aufgabe durch Klicken in die Zelle und gleichzeitiges Drücken von Shift und Enter
Integralrechnung.Integralbegriff.Aufgabe(level=1)#Generiere Aufgabe durch Klicken in die Zelle und gleichzeitiges Drücken von Shift und Enter
Integralrechnung.Integralbegriff.Aufgabe(level=2)#Generiere Aufgabe durch Klicken in die Zelle und gleichzeitiges Drücken von Shift und Enter
Integralrechnung.Integralbegriff.Aufgabe(level=3)#Generiere Aufgabe durch Klicken in die Zelle und gleichzeitiges Drücken von Shift und Enter
Integralrechnung.Integralbegriff.Aufgabe(level=4)#Generiere Aufgabe durch Klicken in die Zelle und gleichzeitiges Drücken von Shift und Enter
Integralrechnung.Integralbegriff.Aufgabe(level=5)#Generiere Aufgabe durch Klicken in die Zelle und gleichzeitiges Drücken von Shift und Enter
Integralrechnung.Integralbegriff.Aufgabe(level=6)#Generiere Aufgabe durch Klicken in die Zelle und gleichzeitiges Drücken von Shift und Enter
Integralrechnung.Integralbegriff.Aufgabe(level=7)#Generiere Aufgabe durch Klicken in die Zelle und gleichzeitiges Drücken von Shift und Enter
Integralrechnung.Integralbegriff.Aufgabe(level=8)#Generiere Aufgabe durch Klicken in die Zelle und gleichzeitiges Drücken von Shift und Enter
Integralrechnung.Integralbegriff.Aufgabe(level=9)#Generiere Aufgabe durch Klicken in die Zelle und gleichzeitiges Drücken von Shift und Enter
Integralrechnung.Integralbegriff.Aufgabe(level=10)Teil B¶
#Generiere Aufgabe durch Klicken in die Zelle und gleichzeitiges Drücken von Shift und Enter
Integralrechnung.Integralbegriff.Aufgabe(level=11)#Generiere Aufgabe durch Klicken in die Zelle und gleichzeitiges Drücken von Shift und Enter
Integralrechnung.Integralbegriff.Aufgabe(level=12)#Generiere Aufgabe durch Klicken in die Zelle und gleichzeitiges Drücken von Shift und Enter
Integralrechnung.Integralbegriff.Aufgabe(level=13)