book.mathe.studien.cloud

Eigenschaften von Vektoren¶

Handwerkszeug für dieses Notebook:¶

Rechenoperationen:

Multiplikation: *

Division und Brüche: /

Eingabe von Potenzen: **

Eingabe eines Kommas als Punkt: .

Eine Zelle ausführen: Enter und Shift gleichzeitig

Egal, wo Sie sich im Notebook befinden: Sie können in eine neue Codezelle immer Spickzettel() schreiben und die Zelle ausführen. Dann erhalten Sie das Handwerkszeug für das Notebook nochmals direkt.

Definition¶

Ein Vektor ist eine Größe, die in der Mathematik mittels Betrag (Länge) und Richtung charakterisiert ist. In der Anwendung kommt noch die Maßeinheit dazu.

Eine vektorielle Größe wird mit einem Pfeil über dem Symbol $\vec{𝒂}$ oder fett dargestellt: 𝒂.

Beispiele für vektorielle Größen sind: Kraft $\mathbf{\vec{𝐹}}$ , Weg bzw. Strecke $\mathbf{\vec{s}}$ , Geschwindigkeit $\mathbf{\vec{v}}$ , Beschleunigung $\mathbf{\vec{𝒂}}$ , Drehmoment $\mathbf{\vec{M}}$ , usw.

Darstellung eines Vektors¶

Ein Vektor in einer Ebene besitzt zwei Komponenten. Damit handelt es sich um einen zweidimensionalen Vektor :$\ \ $ $\vec{v}=\left(\begin{matrix}v_{x}\\ v_{y} \end{matrix}\right)$

Mit den Komponenten eines Vektors kann die Länge des Vektors berechnet werden.

Zur Darstellung von zwei- und dreidimensionalen Vektoren sehen Sie sich gerne das Video des studiVEMINT-Projekts der Universität Paderborn an: https://youtu.be/MVRqdNIZixQ

Aufgaben¶

Generieren Sie sich Aufgaben zum Üben, indem Sie in die folgenden Zellen klicken und Shift und Enter gleichzeitig gedrückt halten. Bearbeiten Sie die Aufgaben dann mit Stift und Papier und geben Ihre Lösung ein.

Graphische Darstellung: Vektorkomponenten aus der Grafik bestimmen

Teil A¶

#Klicken Sie in die Zelle und halten Sie gleichzeitig Shift und Enter gedrück, um die Aufgabe mit Level 1 zu erhalten
Vektorrechnung.Vektorkomponenten.Aufgabe(level=1)

#Klicken Sie in die Zelle und halten Sie gleichzeitig Shift und Enter gedrück, um die Aufgabe mit Level 2 zu erhalten
Vektorrechnung.Vektorkomponenten.Aufgabe(level=2)

#Klicken Sie in die Zelle und halten Sie gleichzeitig Shift und Enter gedrück, um die Aufgabe mit Level 3 zu erhalten
Vektorrechnung.Vektorkomponenten.Aufgabe(level=3)

#Klicken Sie in die Zelle und halten Sie gleichzeitig Shift und Enter gedrück, um die Aufgabe mit Level 4 zu erhalten
Vektorrechnung.Vektorkomponenten.Aufgabe(level=4)

Berechnung der Vektorkomponenten

Teil A¶

#Klicken Sie in die Zelle und halten Sie gleichzeitig Shift und Enter gedrück, um die Aufgabe mit Level 1 zu erhalten
Vektorrechnung.Richtungsvektoren.Aufgabe(level=1)

#Klicken Sie in die Zelle und halten Sie gleichzeitig Shift und Enter gedrück, um die Aufgabe mit Level 2 zu erhalten
Vektorrechnung.Richtungsvektoren.Aufgabe(level=2)

#Klicken Sie in die Zelle und halten Sie gleichzeitig Shift und Enter gedrück, um die Aufgabe mit Level 3 zu erhalten
Vektorrechnung.Richtungsvektoren.Aufgabe(level=3)

#Klicken Sie in die Zelle und halten Sie gleichzeitig Shift und Enter gedrück, um die Aufgabe mit Level 4 zu erhalten
Vektorrechnung.Richtungsvektoren.Aufgabe(level=4)

Länge eines Vektors¶

Die Länge eines zweidimensionalen Vektors $\vec{v}=\left(\begin{matrix}v_{x}\\ v_{y} \end{matrix}\right)$ wird beschrieben mit: $|\vec{v}|=\sqrt{v_{x}^2+ v_{y}^2}$
Diese Formel ergibt sich direkt aus der Anwendung des Satzes des Pythagoras auf das Dreieck, das durch den Vektor und seine Projektionen auf die $x$- und $y$-Achse gebildet wird.

Beispiel:
Berechnung der Länge des Vektors $\mathbf{\vec{AB}}$ aus der nachfolgenden Grafik:

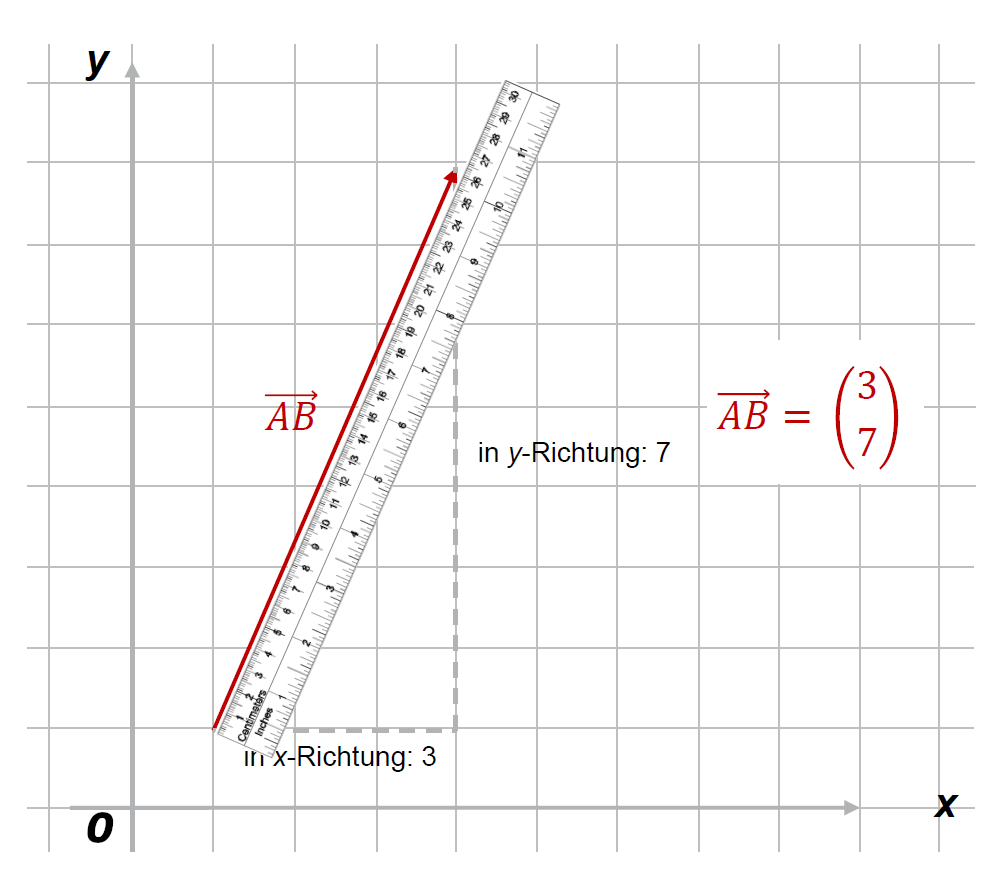
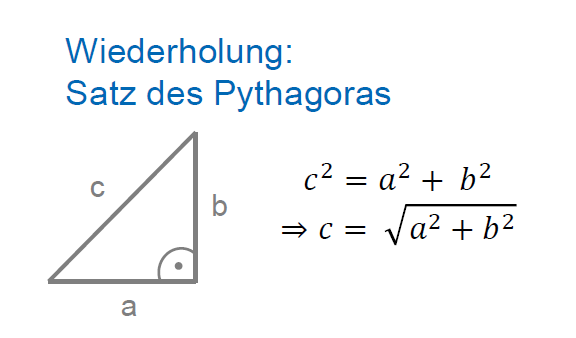
Das Dreieck in der rechten Abbildung kann links identifiziert werden. Es wird durch den Vektor $\vec{AB}$ und dessen $x$ - und $y$ - Komponente aufgespannt:
$c=|\vec{AB}|$ , $a=3$ und $b=7$ .

Die Anwendung des Satzes von Pythagoras ergibt die Länge des Vektors $\vec{AB}$ :
$|\vec{AB}|= \sqrt{3^2+7^2}=\sqrt{58}\simeq 7,6$ .

Aufgaben¶

Generieren Sie sich wieder Aufgaben zum Üben, indem Sie in die folgenden Zellen klicken und gleichzeitig Shift und Enter gedrückt halten.

Teil A¶

#Klicken Sie in die Zelle und halten Sie gleichzeitig Shift und Enter gedrück, um die Aufgabe mit Level 1 zu erhalten
Vektorrechnung.Betrag.Aufgabe(level=1)

#Klicken Sie in die Zelle und halten Sie gleichzeitig Shift und Enter gedrück, um die Aufgabe mit Level 2 zu erhalten
Vektorrechnung.Betrag.Aufgabe(level=2)

#Klicken Sie in die Zelle und halten Sie gleichzeitig Shift und Enter gedrück, um die Aufgabe mit Level 3 zu erhalten
Vektorrechnung.Betrag.Aufgabe(level=3)

#Klicken Sie in die Zelle und halten Sie gleichzeitig Shift und Enter gedrück, um die Aufgabe mit Level 4 zu erhalten
Vektorrechnung.Betrag.Aufgabe(level=4)

Eigenschaften von Vektoren¶

Der Betrag (die Länge) eines Vektores ist immer größer gleich Null: $\vert \vec{a} \vert \ge 0$

Zwei Vektoren gleicher Richung nennt man parallel.

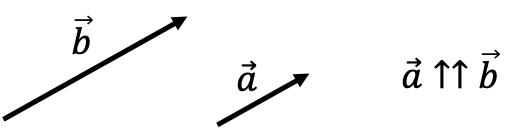
Zwei Vektoren entgegengesetzter Richung nennt man anti-parallel.

Der inverse Vektor hat ein negatives Vorzeichen und kehrt lediglich die Richtung des Vektors um.

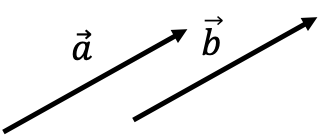
Zwei Vektoren $\vec{a}$ und $\vec{b}$ werden als gleich angesehen, d.h. $ \vec{a} = \vec{b} $, wenn sie in Betrag und Richtung übereinstimmen.

Im Video “Was ist der Betrag eines Vektors” des studiVEMINT-Projekts der Universität Paderborn werden Betrag und Länge nochmal genau erklärt: https://youtu.be/gUTz0io7PTw

Spezielle Vektoren¶

Es gibt im Wesentlichen drei Haupttypen von speziellen Vektoren :

Ortsvektoren sind im
Ursprung verankert
Nullvektoren haben die Länge Null
Einheitsvektoren haben die Länge Eins .

1. Ortsvektoren :

Ein Vektor, der im Ursprung des Koordinatensystems verankert ist, heißt Ortsvektor.

Er gibt die genaue Position eines Punktes in einem gewählten Koordinatensystem an.

Der Ortsvektor $\mathbf{\vec{r}(P)=\vec{OP}}$ führt vom Koordinatenursprung O zum Punkt P.

Beispiele:

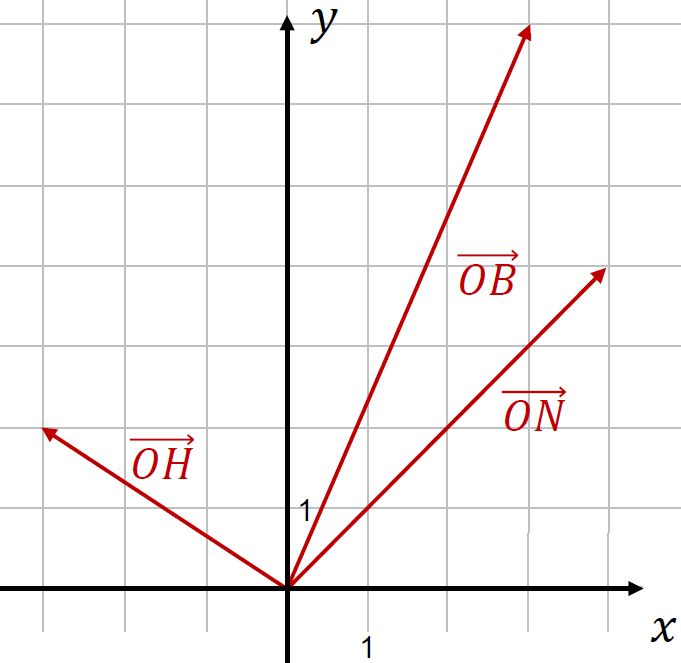
In der folgenden Grafik sind drei Ortsvektoren eingezeichnet:
Ein Ortsvektor zum Punkt B: $\left(\begin{matrix}3\\ 7 \end{matrix}\right)$
Ein Ortsvektor zum Punkt N: $\left(\begin{matrix}4\\ 4 \end{matrix}\right)$
Ein Ortsvektor zum Punkt H: $\left(\begin{matrix}-3\\ 2 \end{matrix}\right)$

2. Nullvektoren:

Der (einzige) Vektor der Länge Null ist der Nullvektor: $\mathbf{|\vec{0}|=0}$ . Für ihn lässt sich keine Richtung angeben, da Anfangs-und Endpunkt zusammenfallen.

3. Einheitsvektoren:
Ein Einheitsvektor ist ein Vektor mit der Länge Eins: $\mathbf{|\vec{e}|=1}$.

Beispiel:
Ein typisches Beispiel für Einheitsvektoren sind die Basisvektoren $\mathbf{\vec{e_x}}$ und $\mathbf{\vec{e_y}}$ . Sie bilden das zweidimensionale Koordinatensystem und geben dieRichtung der $x$ - und $y$ -Achse an.

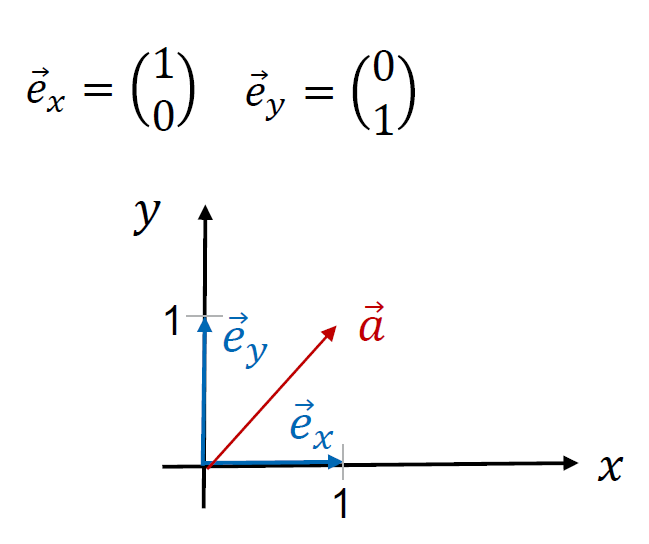
Interaktive Darstellung von 2D Vektoren¶

Die folgende Simulation “2D erkunden” bietet die Möglichkeit, zweidimensionale Vektoren zu untersuchen.
Führen Sie die folgende Zelle aus, indem Sie Shift und Enter gleichzeitig gedrückt halten. Dann sehen Sie die Demo.
Klicken Sie dann auf “2D erkunden”.

#Halten Sie gleichzeitig Shift und Enter gedrückt, um die Demo zu sehen
Demo.Vektoreigenschaften()

Es genügt, den Vektor $\mathbf{\vec{a}}$ , $\mathbf{\vec{b}}$ oder $\mathbf{\vec{c}}$ aus dem Kasten rechts in die Grafik zu schieben, um seine Eigenschaften zu sehen.
Durch Anklicken des Endpunktes des Vektors ist es auch möglich, die Länge und die Richtung des Vektors zu ändern.
Die vier Kästchenoberhalb der Grafik zeigen die Länge, den Winkel zwischen dem Vektor und der $x$ -Achse sowie die $x$ - und $y$ -Komponente des zweidimensionalen Vektors.

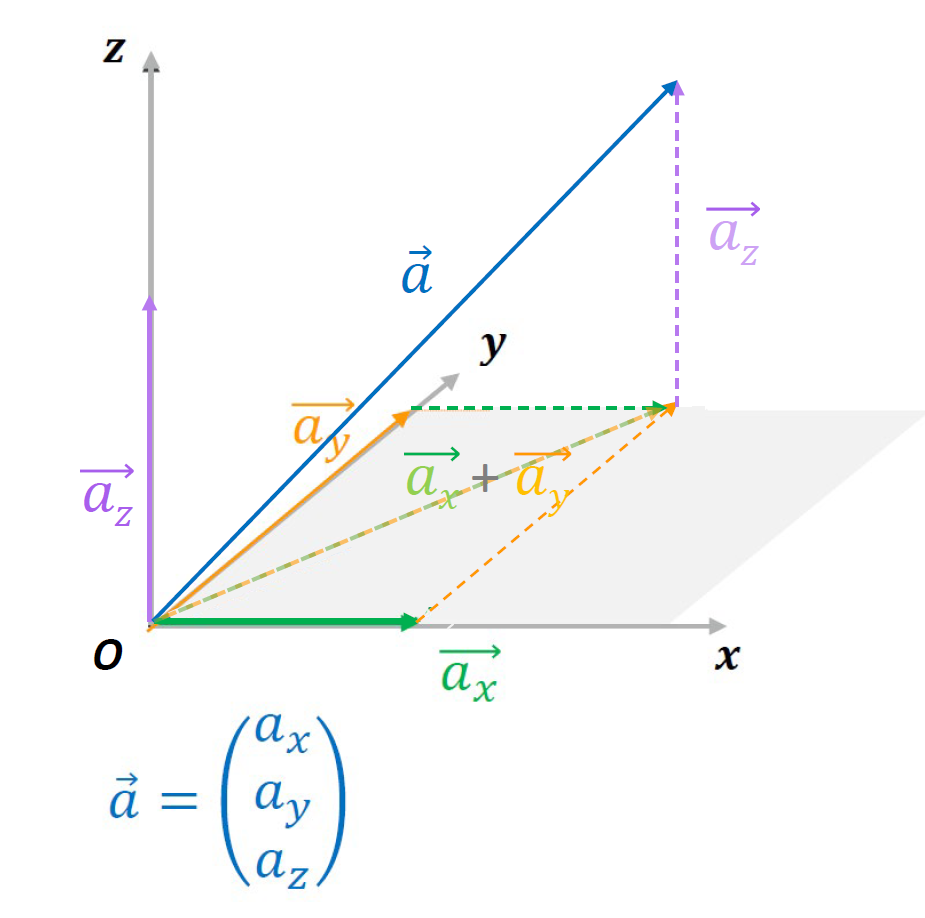
Vektoren in drei Dimensionen¶

Von 2D nach 3D es bleibt (fast) alles gleich:
Ein Vektor in 3D besitzt drei Komponenten. Es handelt sich um einen dreidimensionalen Vektor : $\ $ $\vec{a}=\left(\begin{matrix}a_{x}\\ a_{y} \\ a_{z} \end{matrix}\right)$.
Die Länge eines dreidimensionalen Vektors $\vec{a}$ ist : $|\vec{a}|=\sqrt{a_{x}^2+ a_{y}^2+ a_{z}^2}$

Aufgaben¶

Generieren Sie sich wieder Aufgaben zum Üben, indem Sie in die folgenden Zellen klicken und gleichzeitig Shift und Enter gedrückt halten.

Teil A¶

#Klicken Sie in die Zelle und halten Sie gleichzeitig Shift und Enter gedrück, um die Aufgabe mit Level 5 zu erhalten
Vektorrechnung.Betrag.Aufgabe(level=5)