Skip to article frontmatterSkip to article content

Rechenoperationen

Handwerkszeug für dieses Notebook:

Rechenoperationen:

Multiplikation:  *

Division und Brüche:  /

Eingabe von Potenzen:  **

Eingabe eines Kommas als Punkt:  .

Eine Zelle ausführen:  Enter und Shift gleichzeitig

Egal, wo Sie sich im Notebook befinden: Sie können in eine neue Codezelle immer Spickzettel() schreiben und die Zelle ausführen. Dann erhalten Sie das Handwerkszeug für das Notebook nochmals direkt.

Addition von Vektoren

Vektoren können in beliebiger Reihenfolge addiert werden (Kommutativgesetz):
$\vec{a} + \vec{b} = \left(\begin{matrix}a_{x}\\ a_{y} \end{matrix}\right)+ \left(\begin{matrix}b_{x}\\ b_{y} \end{matrix}\right) = \left(\begin{matrix}a_{x}+b_{x}\\ a_{y}+b_{y} \end{matrix}\right)$.

Beispiel:
Rechnerische und graphische Addition zweier Vektoren a⃗=(21)\vec{a} = \left(\begin{matrix}2\\ 1 \end{matrix}\right) und b⃗=(2−2) \vec{b} =\left(\begin{matrix}2\\ -2 \end{matrix}\right)
Rechnerisch: a⃗+b⃗=(21)+(2−2)=(2+21−2)=(4−1)=b⃗+a⃗\vec{a} + \vec{b} = \left(\begin{matrix}2\\ 1 \end{matrix}\right)+ \left(\begin{matrix}2\\ -2 \end{matrix}\right) = \left(\begin{matrix}2+2\\ 1-2 \end{matrix}\right) =\left(\begin{matrix}4\\ -1 \end{matrix}\right) =\vec{b} +\vec{a}
Graphisch:

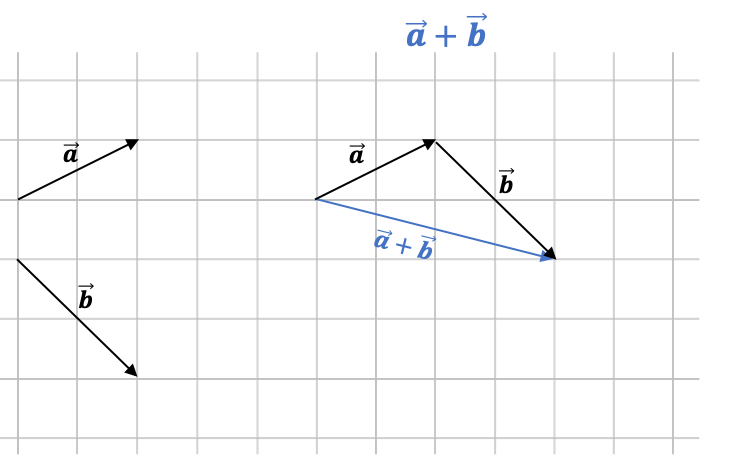
Subtraktion von Vektoren

Die Subtraktion von Vektoren ist dasselbe wie die Addition des inversen Vektors:

\vec{a}- \vec{b} =\vec{a} + (\vec{-b})= \left(\begin{matrix}a_{x}-b_{x}\\ a_{y}-b_{y} \end{matrix}\right).

Beispiel:
Rechnerische und graphische Addition zweier Vektoren a⃗=(21)\vec{a} = \left(\begin{matrix}2\\ 1 \end{matrix}\right) und b⃗=(2−2) \vec{b} = \left(\begin{matrix}2\\ -2 \end{matrix}\right)
Rechnerisch: a⃗−b⃗=(21)−(2−2)=(2−21−(−2))=(03)\vec{a} - \vec{b} = \left(\begin{matrix}2\\ 1 \end{matrix}\right)- \left(\begin{matrix}2\\ -2 \end{matrix}\right) = \left(\begin{matrix}2-2\\ 1-(-2) \end{matrix}\right) =\left(\begin{matrix}0\\ 3 \end{matrix}\right)
Graphisch:

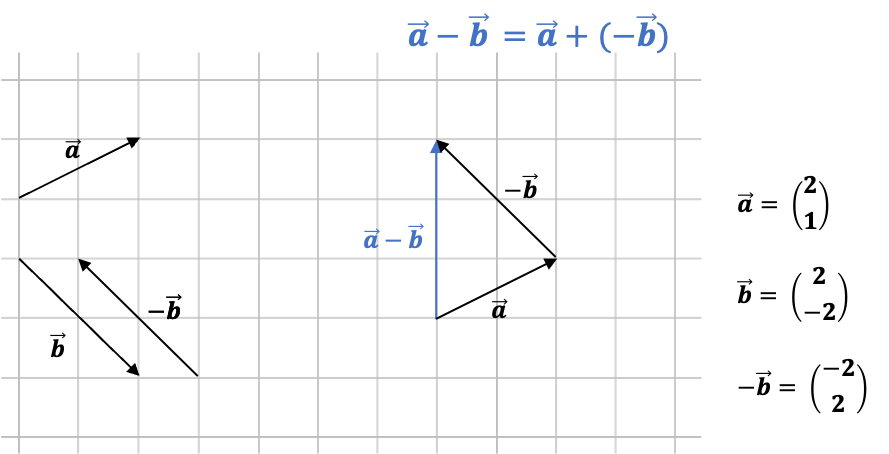
Aufgaben

Generieren Sie sich Aufgaben zum Üben, indem Sie in die folgenden Zellen klicken und Shift und Enter gleichzeitig gedrückt halten. Bearbeiten Sie die Aufgaben dann mit Stift und Papier und geben Ihre Lösung ein.

Teil A
#Klicken Sie in die Zelle und halten Sie gleichzeitig Shift und Enter gedrück, um die Aufgabe mit Level 1 zu erhalten
Vektorrechnung.Rechenoperationen.Aufgabe(level=1)
#Klicken Sie in die Zelle und halten Sie gleichzeitig Shift und Enter gedrück, um die Aufgabe mit Level 2 zu erhalten
Vektorrechnung.Rechenoperationen.Aufgabe(level=2)

Versuch: graphische Addition und Subtraktion von Vektoren

Mit der folgenden Demo können Sie graphisch Vektoren addieren und subtrahieren. Klicken Sie dazu einfach in die folgende Zelle und führen diese aus, indem Sie Shift und Enter gleichzeitig gedrückt halten.

#Klicken Sie in die Zelle und halten Sie gleichzeitig Shift und Enter gedrückt
Demo.GraphischeAddition()

Skalarmultiplikation: Verlängern und verkürzen von Vektoren

Die Multiplikation eines Vektors $ \vec{a} = \left(\begin{matrix}a_{x}\\ a_{y} \end{matrix}\right)$ mit einem Skalar $ \lambda$ erfolgt komponentenweise:
$ \lambda \cdot \vec{a}=\left(\begin{matrix}\lambda\cdot a_{x}\\ \lambda \cdot a_{y} \end{matrix}\right)$ mit $ \lambda ∈ℝ $
Also: $ |\lambda \cdot \vec{a}|= |\lambda|\cdot|\vec{a}|$

Die Skalarmultiplikation führt immer zu einem parallelen oder antiparallelen Vektor:
a. Multiplikation mit ∣λ>1∣|\lambda>1| verlängert (streckt) den Vektor
b. Multiplikation mit ∣λ<1∣|\lambda<1| verkürzt (staucht) den Vektor
c. Multiplikation mit λ<0\lambda<0 kehrt die Richtung des Vektors um

Beispiel:

Gegeben ist der Vektor \vec{a} = \left(\begin{matrix}1\\ 2 \end{matrix}\right). Dieser wird mit einem Skalar λ\lambda multipliziert.

Rechnerische Multiplikation


a. Verlängerung: Für \lambda=2 gilt λ⋅a⃗=2⋅a⃗=(2⋅12⋅2)=\lambda \cdot \vec{a} = 2 \cdot \vec{a} = \left(\begin{matrix} 2 \cdot 1\\ 2 \cdot 2 \end{matrix}\right)= \left(\begin{matrix}2\\ 4 \end{matrix}\right)
b. Verkürzung: Für \lambda=\frac{1}{2} gilt λ⋅a⃗=12⋅a⃗=(12⋅112⋅2)=\lambda \cdot \vec{a} =\frac{1}{2} \cdot \vec{a} = \left(\begin{matrix} \frac{1}{2} \cdot 1\\ \frac{1}{2} \cdot 2 \end{matrix}\right)= \left(\begin{matrix}\frac{1}{2}\\ 1 \end{matrix}\right)
c. Umkehrung der Richtung: Für \lambda=-1 gilt λ⋅a⃗=((−1)⋅1(−1)⋅2)=\lambda \cdot \vec{a} = \left(\begin{matrix} (-1)\cdot 1\\ (-1) \cdot 2 \end{matrix}\right)= \left(\begin{matrix}- 1\\ -2 \end{matrix}\right)= -\vec{a}

Graphische Multiplikation:
\vec{a} : grauer Vektor, Verlängerung für \lambda=2 : blauer Vektor ,Verkürzung für \lambda=\frac{1}{2} : roter Vektor, Umkehrung der Richtung für \lambda=-1 : grüner Vektor

Zur Addition, Subtraktion und Skalarmultiplikation finden Sie unter https://youtu.be/RqrbuQ5wCKE ein Video des studiVEMINT-Projekts der Universität Paderborn.

Aufgaben

Generieren Sie sich Aufgaben zum Üben, indem Sie in die folgenden Zellen klicken und Shift und Enter gleichzeitig gedrückt halten. Bearbeiten Sie die Aufgaben dann mit Stift und Papier und geben Ihre Lösung ein.

Teil A
#Klicken Sie in die Zelle und halten Sie gleichzeitig Shift und Enter gedrück, um die Aufgabe mit Level 3 zu erhalten
Vektorrechnung.Rechenoperationen.Aufgabe(level=3)

Der Einheitsvektor

Der Einheitsvektor des Vektors $ \vec{a} =\left(\begin{matrix}a_{x}\\ a_{y} \end{matrix}\right)$ wird gebildet, indem $ \vec{a}$ durch seine Länge geteilt wird:
$$\mathbf{\vec{e_a}}= \frac{\vec{a}}{|\vec{a}|} = \frac{1}{|\vec{a}|} \cdot \vec{a} $$
Man sagt auch: Der Vektor $ \vec{a}$ wird „auf 1 normiert“.

Die Länge des Vektors ist gegeben durch : ∣a⃗∣=ax2+ay2|\vec{a}|=\sqrt{a_{x}^2+ a_{y}^2}.
Ein Vektor a⃗ \vec{a} wurde auf 1 normiert, wenn er mit dem Skalar λ=1∣a⃗∣\lambda= \frac{1}{|\vec{a}|} multipliziert wurde: ea⃗=λ⋅a⃗\mathbf{\vec{e_a}}= \lambda \cdot {\vec{a}}

Bei der Normierung ist λ\lambda immer positiv, so dass die Richtung des Vektors a⃗ \vec{a} gleich bleibt.

Beispiel:
Der Vektor a⃗=(34) \vec{a} = \left(\begin{matrix}3\\ 4 \end{matrix}\right) soll normiert werden.

Länge: ∣a⃗∣=32+42=25=5|\vec{a}|=\sqrt{3^2+4^2}=\sqrt{25}=5
Der normierte Vektor ist : ea⃗=15(34)=(3545) \vec{e_a}=\frac{1}{5}\left(\begin{matrix}3\\ 4 \end{matrix}\right)=\left(\begin{matrix}\frac{3}{5}\\ \frac{4}{5}\end{matrix}\right)
Die Länge des normierten Vektors ist: ∣ea⃗∣=(35)2+(45)2=32+4252=32+4252=255=1|\vec{e_a}|=\sqrt{(\frac{3}{5})^2+(\frac{4}{5})^2}=\sqrt{\frac{3^2+4^2}{5^2}}=\frac{\sqrt{3^2+4^2}}{\sqrt{5^2}}=\frac{\sqrt{25}}{5}=1


Linearkombinationen

Die Skalarmultiplikation von Vektoren in Kombination mit der Addition und/oder Subtraktion eines Vektors wird als Linearkombination bezeichnet.
Die Linearkombination zweier Vektoren $\vec{a}$ und $\vec{b}$ erfolgt komponenteweise:
$ \vec{c} =\lambda \cdot \vec{a}+\mu \cdot \vec{b}= \left(\begin{matrix}\lambda\cdot a_{x}+\mu \cdot b_{x}\\ \lambda \cdot a_{y} +\mu \cdot b_{y} \end{matrix}\right)$ mit $ \lambda , \mu ∈ℝ $

Also: für λ=μ\lambda =\mu ,     λ⋅(a⃗+b⃗)=λ⋅a⃗+λ⋅b⃗ \lambda \cdot (\vec{a}+ \vec{b})= \lambda \cdot \vec{a}+\lambda \cdot \vec{b}
\hspace{0.8cm} für a⃗=b⃗\vec{a}=\vec{b} ,     (λ+μ)⋅a⃗=λ⋅a⃗+μ⋅a⃗ (\lambda+\mu) \cdot \vec{a} = \lambda \cdot \vec{a}+\mu \cdot \vec{a}

Anwendung: Bestimmung eines Richtungsvektors aus Ortsvektoren

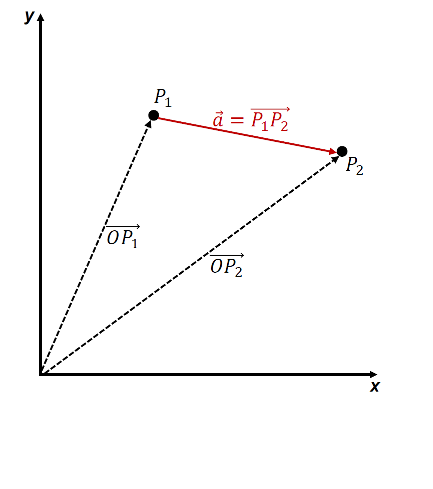
Gegeben sind die Punkte P1(x1/y1) P_1 (x_1/y_1) und P2(x2/y2)P_2 (x_2/y_2)
mit den Ortsvektoren OP1⃗=(x1y1) \vec{OP_1} = \left(\begin{matrix}x_1\\ y_1 \end{matrix}\right) und OP2⃗=(x2y2) \vec{OP_2} = \left(\begin{matrix}x_2\\ y_2 \end{matrix}\right)
und Vektor \vec{a} durch den Anfangspunkt P1(x1/y1) P_1 (x_1/y_1) und den Endpunkt P2(x2/y2) P_2 (x_2/y_2):

Der Vektor \vec{a} ergibt sich damit aus:

a⃗=P1P2⃗=P1O⃗+OP2⃗=−OP1⃗+OP2⃗=(x2−x1y2−y1)=(axay) \vec{a} = \vec{P_1P_2} = \vec{P_1O} + \vec{OP_2} = - \vec{OP_1} + \vec{OP_2} = \left(\begin{matrix}x_2 - x_1\\ y_2 - y_1 \end{matrix}\right) = \left(\begin{matrix}a_x\\ a_y \end{matrix}\right)

Aufgaben

Generieren Sie sich Aufgaben zum Üben, indem Sie in die folgenden Zellen klicken und Shift und Enter gleichzeitig gedrückt halten. Bearbeiten Sie die Aufgaben dann mit Stift und Papier und geben Ihre Lösung ein.

Teil A
#Klicken Sie in die Zelle und halten Sie gleichzeitig Shift und Enter gedrückt, um die Aufgabe mit Level 4 zu erhalten
Vektorrechnung.Rechenoperationen.Aufgabe(level=4)
#Klicken Sie in die Zelle und halten Sie gleichzeitig Shift und Enter gedrückt, um die Aufgabe mit Level 5 zu erhalten
Vektorrechnung.Rechenoperationen.Aufgabe(level=5)
#Klicken Sie in die Zelle und halten Sie gleichzeitig Shift und Enter gedrückt, um die Aufgabe mit Level 6 zu erhalten
Vektorrechnung.Rechenoperationen.Aufgabe(level=6)

Berechnungen mit Ortsvektoren

#Klicken Sie in die Zelle und halten Sie gleichzeitig Shift und Enter gedrück, um die Aufgabe zu erhalten
Demo.Ortsvektoren()
#Klicken Sie in die Zelle und halten Sie gleichzeitig Shift und Enter gedrück, um die Aufgabe zu erhalten
Demo.Richtungsvektoren()

Anwendungsaufgaben: Flugzeuglandung im Wind

Teil A
Windböen parallel zur Flugbahn des Flugzeugs
#Klicken Sie in die Zelle und halten Sie gleichzeitig Shift und Enter gedrück, um die Aufgabe mit Level 1 zu erhalten
Vektorrechnung.Anwendung_Flugzeug.Aufgabe(level=1)
Windböen senkrecht zur Flugbahn des Flugzeugs ($v_x=v_{py}=0$)
#Klicken Sie in die Zelle und halten Sie gleichzeitig Shift und Enter gedrück, um die Aufgabe mit Level 2 zu erhalten
Vektorrechnung.Anwendung_Flugzeug.Aufgabe(level=2)
Teil B
Windböen senkrecht zur Flugbahn des Flugzeugs ($v_y=v_{px}=0$)
#Klicken Sie in die Zelle und halten Sie gleichzeitig Shift und Enter gedrück, um die Aufgabe mit Level 3 zu erhalten
Vektorrechnung.Anwendung_Flugzeug.Aufgabe(level=3)
Windböen aus allen Richtungen
#Klicken Sie in die Zelle und halten Sie gleichzeitig Shift und Enter gedrück, um die Aufgabe mit Level 4 zu erhalten
Vektorrechnung.Anwendung_Flugzeug.Aufgabe(level=4)
Flugbahn des Flugzeugs in alle Richtungen
#Klicken Sie in die Zelle und halten Sie gleichzeitig Shift und Enter gedrück, um die Aufgabe mit Level 5 zu erhalten
Vektorrechnung.Anwendung_Flugzeug.Aufgabe(level=5)
Flugbahn des Flugzeugs und Windböen in und aus allen Richtungen
#Klicken Sie in die Zelle und halten Sie gleichzeitig Shift und Enter gedrück, um die Aufgabe mit Level 6 zu erhalten
Vektorrechnung.Anwendung_Flugzeug.Aufgabe(level=6)
Vektorrechnung
Definition Vektoren
Vektorrechnung
Vektorzerlegung