Anwendungen der Vektorrechnung¶
Handwerkszeug für dieses Notebook:¶
Rechenoperationen:
Multiplikation: *
Division und Brüche: /
Eingabe von Potenzen: **
Eingabe eines Kommas als Punkt: .
Eine Zelle ausführen: Enter und Shift gleichzeitig
Egal, wo Sie sich im Notebook befinden: Sie können in eine neue Codezelle immer Spickzettel() schreiben und die Zelle ausführen. Dann erhalten Sie das Handwerkszeug für das Notebook nochmals direkt.
Simulation zur Orthogonalität zweier Vektoren¶
Klicken Sie in die folgende Zelle und führen Sie aus, indem Sie Shift und Enter gleichzeitig gedrückt halten. Damit öffnet sich im Notebook die Simulation zur Orthogonalität zweier Vektoren. Lesen Sie den Text dort und beantworten Sie anschließend die Fragen.
Falls dies bei Ihnen nicht funktionieren sollte, können Sie alternativ auf den Link in der darauffolgenden Zelle klicken und die Simulation in einem neuen Tab öffnen.
Beachten Sie, dass die Formel 𝑟𝑎𝑑 für den Winkel in dem Applet nur für 𝛼 zwichen 0° und 180° gültig ist.
from IPython.display import IFrame
IFrame("https://www.geogebra.org/m/cwvmhvn8", 1000,1000)Falls die Simulation mit dem Ausführen der oberen Zelle nicht funktioniert, können Sie auf den Link https://
Anwendung: Kräfte in der Statik¶
a. Winkel zwischen Vektoren (z.B. zwischen Kräften in der Statik)
Gegeben sind zwei Kräfte und . Wie groß ist der Winkel zwischen ihnen?
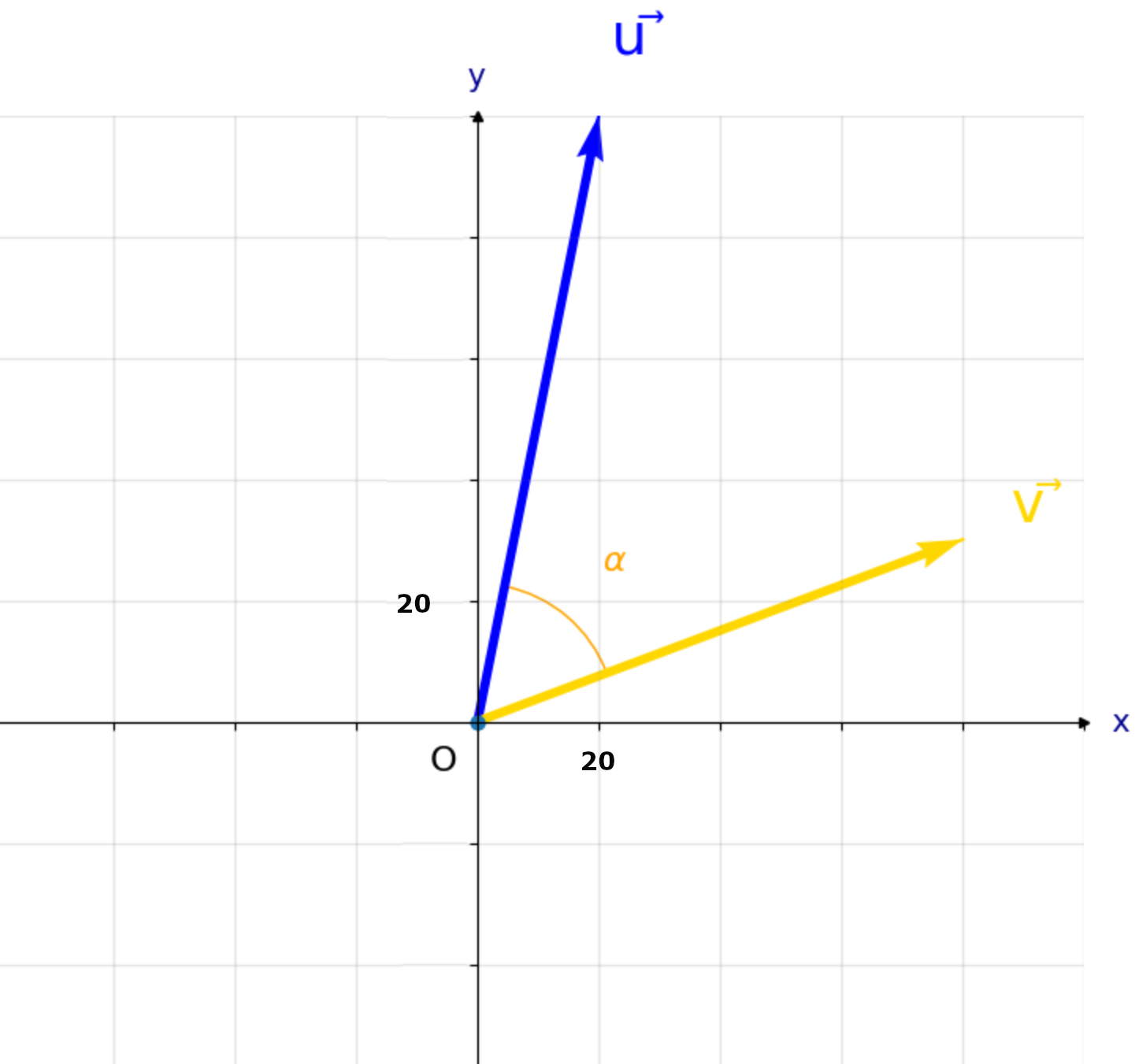
Der Winkel zwischen und ist also:
b. Berechnung der verrichteten Arbeit in der Physik
In der Physik wird die Arbeit durch das Skalarprodukt aus Kraft und Strecke mit ermittelt. Die Einheit der Arbeit ist
Ein Spediteur schiebt eine Kiste mit der Kraft
eine Rampe hinauf .
Gesucht ist die Arbeit , die von der Kraft verrichtet wird.
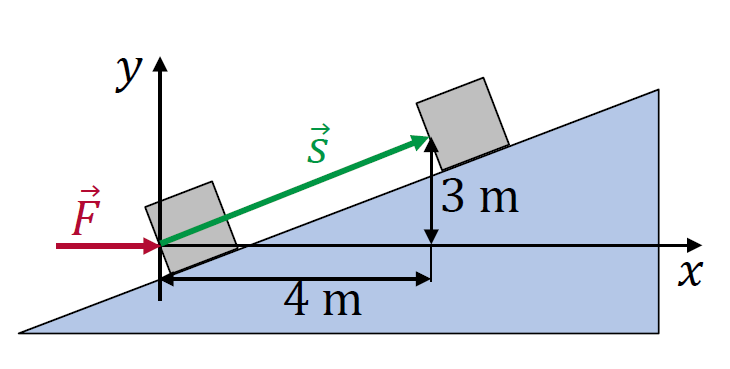
Berechnung von :
Anwendung: Kiste auf einer Rampe¶
Ein Spediteur schiebt eine Kiste mit der Kraft längs eines Weges eine Rampe unter dem Winkel hinauf.
Der Energieunterschied des Systems entspricht der verrichteten Arbeit , die von der Kraft verrichtet wird.

Aufgaben¶
Generieren Sie sich Aufgaben zum Üben, indem Sie in die folgenden Zellen klicken und Shift und Enter gleichzeitig gedrückt halten. Bearbeiten Sie die Aufgaben dann mit Stift und Papier und geben Ihre Lösung ein.
Teil B¶
Level 1: Horizontale Kraft und Weg (in die gleiche Richtung)
#Klicken Sie in die Zelle und drücken Sie anschließend gleichzeitig Shift und Enter, um die Aufgabe mit Level 1 zu erhalten
Vektorrechnung.Anwendung_Skalarprodukt.Aufgabe(level=1)Level 2: Horizontale (Reibungs-)Kraft und Weg in entgegengesetzter Richtung
#Klicken Sie in die Zelle und drücken Sie anschließend gleichzeitig Shift und Enter, um die Aufgabe mit Level 2 zu erhalten
Vektorrechnung.Anwendung_Skalarprodukt.Aufgabe(level=2)Level 3: Horizontale Kraft
#Klicken Sie in die Zelle und drücken Sie anschließend gleichzeitig Shift und Enter, um die Aufgabe mit Level 3 zu erhalten
Vektorrechnung.Anwendung_Skalarprodukt.Aufgabe(level=3)Level 4: Kraft und Weg parallel zueinander
#Klicken Sie in die Zelle und drücken Sie anschließend gleichzeitig Shift und Enter, um die Aufgabe mit Level 4 zu erhalten
Vektorrechnung.Anwendung_Skalarprodukt.Aufgabe(level=4)Level 5: Allgemeiner Fall
#Klicken Sie in die Zelle und drücken Sie anschließend gleichzeitig Shift und Enter, um die Aufgabe mit Level 5 zu erhalten
Vektorrechnung.Anwendung_Skalarprodukt.Aufgabe(level=5)