Skip to article frontmatterSkip to article content
Handwerkszeug für dieses Notebook:

Verwendung eines Punktes als Dezimalzeichen:  .

Trigonometrie

Winkelberechnung am Dreieck

Im rechtwinkligen Dreieck gilt:

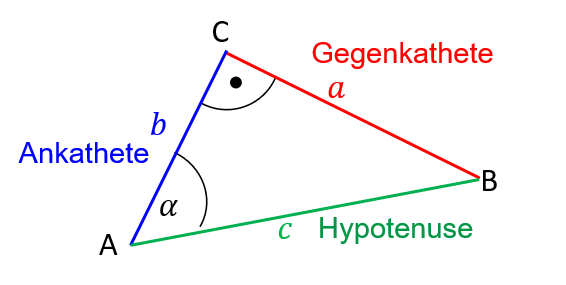
$\sin(\alpha)=\frac{\color{red}{Gegenkathete}}{\color{green}{Hypotenuse}}=\frac{\color{red}{a}}{\color{green}{c}} = \frac{\color{red}{\overline{BC}}}{\color{green}{\overline{AB}}}$

$\cos(\alpha)=\frac{\color{blue}{Ankathete}}{\color{green}{Hypotenuse}}=\frac{\color{blue}{b}}{\color{green}{c}} = \frac{\color{blue}{\overline{AC}}}{\color{green}{\overline{AB}}}$

$\tan(\alpha)=\frac{\color{red}{Gegenkathete}}{\color{blue}{Ankathete}}=\frac{\color{red}{a}}{\color{blue}{b}} = \frac{\color{red}{\overline{BC}}}{\color{blue}{\overline{AC}}}$

$\cot(\alpha)=\frac{\color{blue}{Ankathete}}{\color{red}{Gegenkathete}}=\frac{\color{blue}{b}}{\color{red}{a}} = \frac{\color{blue}{\overline{AC}}}{\color{red}{\overline{BC}}}=\frac{1}{\tan(\alpha)}$

Trigonometrie am Einheitskreis

Visualisierung von $\sin(\alpha)$ und $\cos(\alpha)$

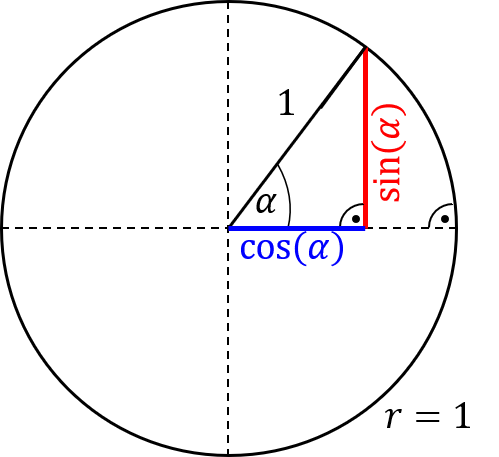Im Einheitskreis lässt sich für beliebige Winkel $\alpha$ jeweils ein rechtwinkliges Dreieck konstruieren, wie es auf der Abbildung rechts gezeigt ist. Die Hypotenuse in diesem rechtwinkligen Dreieck hat die Länge 1. Nach Definition gilt:


$\sin(\alpha)=\frac{Gegenkathete}{Hypotenuse}$


$\cos(\alpha)=\frac{Ankathete}{Hypotenuse}$


Folglich entspricht die Länge der Gegenkathete in dem dargestellten Dreieck direkt $\sin(\alpha)$. Analog dazu lässt sich über die Länge der Ankathete der $\cos(\alpha)$ bestimmen.



Laut dem Satz des Pythagoras gilt:

\color{red}{\sin^2(\alpha)} + \color{blue}{\cos^2(\alpha)} = 1

Variieren Sie in der folgenden Abbildung über den Schieberegler den Winkel α\alpha und beobachten Sie, wie sich das Dreieck und damit verbunden die Werte für sin⁡(α)\sin(\alpha) und cos⁡(α)\cos(\alpha) ändern. Auf der rechten Seite sehen Sie als Ergänzung die Funktionsschaubilder der Funktionen sin⁡(α)\sin(\alpha) (schwarze Linie) und cos⁡(α)\cos(\alpha) (grau gestrichelte Linie). Dort lassen sich ebenfalls die Funktionswerte für den eingestellten Winkel α\alpha ablesen.

# Führen Sie diese Zelle durch gleichzeitiges Drücken von Steuerung und Enter aus, um die Graphik anzuzeigen
Demo.Trigonometrie_am_Einheitskreis()

Eigenschaften und Formeln

Anhand des Einheitskreises lassen sich einige Eigenschaften und Formeln der Sinus- und Kosinus-Funktion veranschaulichen. Wählen Sie im folgenden Plot die jeweilige Formel und machen Sie sich anhand der Abbildung klar, warum dieser Zusammenhang gilt.

# Führen Sie diese Zelle durch gleichzeitiges Drücken von Steuerung und Enter aus, um die Graphik anzuzeigen
Demo.Trigonometrische_Zusammenhaenge()

Die Visualisierung von Sinus, Cosinus und Tangens und Erklärungen dazu gibt es im Video! https://youtu.be/3cSmpWBZG-w

Visualisierung von $\tan(\alpha)$ am Einheitskreis

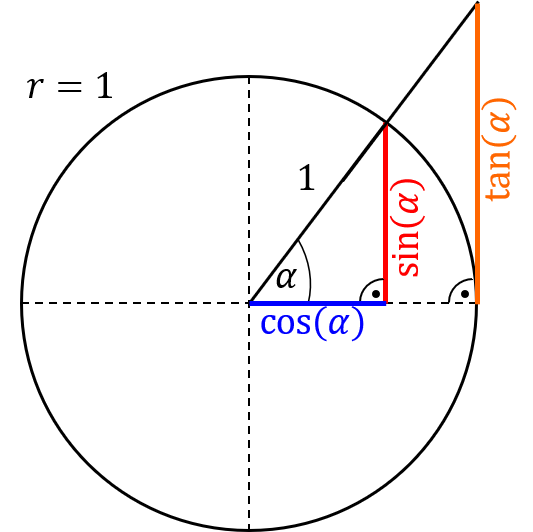Herleitung des Tangens



Laut dem 2. Strahlensatz gilt:


$\frac{\sin(\alpha)}{\tan(\alpha)}=\frac{\cos(\alpha)}{1}$



Daraus folgt:



$\tan(\alpha)=\frac{\sin(\alpha)}{\cos(\alpha)}=\frac{Gegenkathete}{Ankathete}$


Variieren Sie in der folgenden Abbildung über den Schieberegler den Winkel α\alpha und beobachten Sie, wie sich die Werte für tan⁡(α)\tan(\alpha) ändern. (Da tan⁡(α)\tan(\alpha) für α\alpha=90° und α\alpha=270° bzw. α\alpha=-90° jeweils eine Polstelle besitzt, ist der einzustellende Winkelbereich eingegrenzt.)

# Führen Sie diese Zelle durch gleichzeitiges Drücken von Steuerung und Enter aus, um die Graphik anzuzeigen
Demo.Tangens_am_Einheitskreis()

Spezielle Werte der Winkelfunktionen

Grad0°45°90°180°360°
Rad0$\frac{\pi}{4}$$\frac{\pi}{2}$$\pi$$2\pi$
$\sin(\alpha)$0$\frac{1}{2}\sqrt{2}$100
$\cos(\alpha)$1$\frac{1}{2}\sqrt{2}$0-11
$\tan(\alpha)$01Polstelle00

Aufgaben

Generieren Sie sich nun zum Abschluss noch Übungsaufgaben. Führen Sie die folgende Zelle aus, indem Sie zunächst in die Zelle klicken und dann Steuerung und Enter gleichzeitig drücken.
Dadurch erhalten Sie die Aufgabe der Schwierigkeitsstufe 1. Berechnen Sie anschließend die Lösung der Aufgabe mit Stift und Papier und überprüfen Sie Ihr Ergebnis.

Teil A
# Aufgabe generieren (Schwierigkeitsstufe 1)
Geometrie.Trigonometrie.Aufgabe(level=1)

Generieren Sie sich jetzt über die folgende Code-Zelle eine Aufgabe in der Schwierigkeitsstufe 2.

# Aufgabe generieren (Schwierigkeitsstufe 2)
Geometrie.Trigonometrie.Aufgabe(level=2)

Generieren Sie sich jetzt über die folgende Code-Zelle eine Aufgabe in der Schwierigkeitsstufe 3.

# Aufgabe generieren (Schwierigkeitsstufe 3)
Geometrie.Trigonometrie.Aufgabe(level=3)

Generieren Sie sich jetzt über die folgende Code-Zelle eine Aufgabe in der Schwierigkeitsstufe 4.

Teil B
# Aufgabe generieren (Schwierigkeitsstufe 4)
Geometrie.Trigonometrie.Aufgabe(level=4)
Geometrie
Dreieckseigenschaften
Gleichungen
Lineare Gleichungen