Handwerkszeug für dieses Notebook:¶
Verwendung eines Punktes als Dezimalzeichen: .
Winkel und Winkelmaße¶
Winkel spielen unter anderem in der Physik eine große Rolle. So werden zum Beispiel bei der Reflexion und Brechung von Lichtstrahlen in der Optik Ein- und Ausfallswinkel betrachtet. Ebenso müssen bei der Bestimmung des Kräftegleichgewichts entlang einer schiefen Ebene Winkel betrachtet werden.
Winkel werden immer gegen den Uhrzeigersinn gemessen.

Zur Angabe der Größe eines Winkels können verschiedene Winkelmaße gewählt werden. In der Mathematik verwendet man üblicherweise das Gradmaß und das Bogenmaß.
Gradma߶
Um Winkel anzugeben, die kleiner als 1° sind, werden Bogenminuten und Bogensekunden verwendet. Dabei gilt:
Ein Winkel- oder auch Bogengrad hat 60 Bogenminuten:
Eine Bogenminute hat 60 Bogensekunden:
Bogenma߶
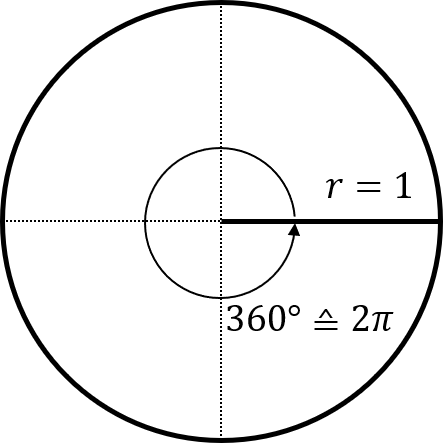 Als Bogenmaß dient die Maßzahl der Länge des Bogens am Einheitskreis. Als Einheitskreis wird in der Mathematik ein Kreis mit Radius 1 bezeichnet. Der Umfang eines beliebigen Kreises mir Radius $r$ ist definiert als $U=2\pi r$. Für den Einheitskreis mit Radius $r=1$ ergibt sich damit der Umfang $U=2\pi$.
Als Bogenmaß dient die Maßzahl der Länge des Bogens am Einheitskreis. Als Einheitskreis wird in der Mathematik ein Kreis mit Radius 1 bezeichnet. Der Umfang eines beliebigen Kreises mir Radius $r$ ist definiert als $U=2\pi r$. Für den Einheitskreis mit Radius $r=1$ ergibt sich damit der Umfang $U=2\pi$.Dabei steht “rad” für Radiant und ist das Einheitenzeichen im Bogenmaß. Dieses Einheitenzeichen wird auch oft weggelassen. Begegnen Sie also einem Winkel, dessen Wert ohne Einheitenzeichen angegeben ist, so ist dieser Winkel im Bogenmaß angegeben.
Analog zu der oberen Überlegung erkennen wir, dass der halbe Einheitskreis die Bogenlänge hat. Es gilt also im Bogenmaß entspricht 180° im Gradmaß. Ein Viertel des Einheitskreises hat die Bogenlänge und entspricht damit 90°. Machen Sie sich diese Zusammenhänge mit Hilfe der folgenden Graphik klar. Verwenden Sie den Schieberegler, um verschiedene Winkel einzustellen, und vergleichen Sie jeweils die Winkelwerte im Grad- und im Bogenmaß.
# Führen Sie diese Zelle durch gleichzeitiges Drücken von Steuerung und Enter aus, um die Graphik anzuzeigen
Demo.Bogenmass()Zusammenfassung der Winkelmaße¶
| Winkelmaß | Maßeinheit | Vollwinkel | Einheitenzeichen | Taschenrechner |
|---|---|---|---|---|
| Gradmaß | Grad | 360° | ° | Deg (für Degree) |
| Bogenminute | 360 60’ | ’ | ||
| Bogensekunde | 360 60 60’’ | ‘’ | ||
| Bogenmaß | Radiant | rad | rad | Rad (für Radiant) |
Bei vielen Taschenrechnern lässt sich noch ein weiteres Winkelmaß einstellen, das oft mit “GRAD” bezeichnet wird. Wenn Sie mehr darüber wissen möchten, dann klicken Sie auf die Eule.
🦉
Umrechnung zwischen Grad- und Bogenma߶
$\varphi = \alpha \cdot \frac{2\pi}{360°}$ oder $\varphi = \alpha \cdot \frac{\pi}{180°}$
Diesen Zusammenhang kann man sich über einen einfachen Dreisatz oder über den 1. Strahlensatz veranschaulichen. Wenn Sie mehr dazu wissen möchten, dann klicken Sie auf die Eule.
🦉
| Winkel im Gradmaß | Winkel im Bogenmaß |
|---|---|
| in ° | in rad |
| 360 | $2\pi$ |
| 1 | $\frac{2\pi}{360}$ |
| $\alpha$ | $\alpha\cdot \frac{2\pi}{360}$ |
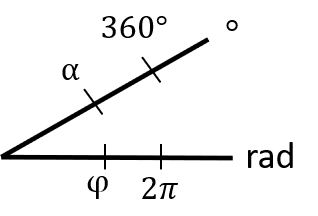 Ein anderer Weg ist die Veranschaulichung über den 1. Strahlensatz. Wir denken uns einfach auf einem der beiden Strahlen die Größen im Gradmaß und auf dem anderen Strahl die Größen im Bogenmaß (siehe Skizze auf der rechten Seite). Nach dem 1. Strahlensatz kann man dann die beiden folgenden Verhältnisse gleich setzen:
Ein anderer Weg ist die Veranschaulichung über den 1. Strahlensatz. Wir denken uns einfach auf einem der beiden Strahlen die Größen im Gradmaß und auf dem anderen Strahl die Größen im Bogenmaß (siehe Skizze auf der rechten Seite). Nach dem 1. Strahlensatz kann man dann die beiden folgenden Verhältnisse gleich setzen:$\quad\frac{\varphi}{2\pi}=\frac{\alpha}{360°}$
Umstellen der Gleichung führt dann ebenfalls auf den oberen Zusammenhang.
Beispiel 1:
Beispiel 2:
Beispiel 3:
Zur Umrechnung zwischen Grad- und Bogenmaß gibt es weitere Erklärungen in unserem Video.
https://
Aufgaben¶
Generieren Sie sich nun wieder Aufgaben zum Üben. Führen Sie die folgende Zelle aus, indem Sie zunächst in die Zelle klicken und dann Steuerung und Enter gleichzeitig drücken. Berechnen Sie anschließend die Lösung der Aufgabe mittels Stift und Papier und überprüfen Sie Ihr Ergebnis.
Teil A¶
# Aufgabe generieren (Schwierigkeitsstufe 1)
Geometrie.Bogenmass.Aufgabe(level=1)Um die Umrechnung vom Bogen- ins Gradmaß zu üben, generieren Sie sich eine Aufgabe mit Hilfe der folgenden Code-Zelle.
# Aufgabe generieren (Schwierigkeitsstufe 2)
Geometrie.Bogenmass.Aufgabe(level=2) Handelt es sich nicht um den Einheitskreis, muss zur Berechnung der Bogenlänge $b_r$ der Radius $r$ des Kreises beachtet werden. Der Umfang des Kreises ist $U=2\pi r$. Die Bogenlänge $b_r$ ist ein Teil der Strecke des Umfangs $U$ und es gilt:
Handelt es sich nicht um den Einheitskreis, muss zur Berechnung der Bogenlänge $b_r$ der Radius $r$ des Kreises beachtet werden. Der Umfang des Kreises ist $U=2\pi r$. Die Bogenlänge $b_r$ ist ein Teil der Strecke des Umfangs $U$ und es gilt:
$b_r = \frac{\alpha}{360°}\cdot 2\pi r$ mit $\alpha$: Winkel im Gradmaß
oder
$b_r = \varphi r$ mit $\varphi$: Winkel im Bogenmaß
Beispiel:
Die Berechnung der Bogenlänge ist mit beiden Formeln möglich:
Direktes Einsetzen in die erste Formel ergibt:
$b_r = \frac{45°}{360°}\cdot 2 \pi \cdot 2\,\text{cm} = \frac{1}{8}\cdot 2 \pi \cdot 2\,\text{cm} = \frac{\pi}{4} \cdot 2\,\text{cm} \approx 1{,}571\,\text{cm}$
Bei Verwendung der zweiten Formel gilt:
Umrechnung des Winkels ins Bogenmaß: $\varphi=\frac{\alpha}{180°}\cdot \pi = \frac{45°}{180°}\cdot \pi = \frac{1}{4}\cdot \pi=\frac{\pi}{4}$
Berechnung der Kreisbogenlänge: $b_r=\frac{\pi}{4}\cdot 2\,\text{cm} \approx 1{,}571\,\text{cm}$
Sehen Sie sich gerne dazu auch das Video an!
https://
Spezielle Winkel und Winkelbereiche¶
| Grad | Rad | Bezeichnung | Skizze |
|---|---|---|---|
| 90° | rechter Winkel |  | |
| 0 bis 90° | 0 bis | spitzer Winkel |  |
| 90° bis 180° | bis | stumpfer Winkel |  |
| 180° bis 360° | bis | überstumpfer Winkel | 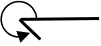 |
Aufgabe¶
Generieren Sie sich nun zum Abschluss noch einmal eine Aufgabe zum Üben. Führen Sie die folgende Zelle aus, indem Sie zunächst in die Zelle klicken und dann Steuerung und Enter gleichzeitig drücken. Berechnen Sie anschließend die Lösung der Aufgabe mit Stift und Papier und überprüfen Sie Ihr Ergebnis.
Teil B¶
# Aufgabe generieren
Geometrie.Bogenmass.Aufgabe(level=3)