book.mathe.studien.cloud

Differentialrechnung¶

Handwerkszeug für dieses Notebook:¶

Rechenoperationen:

Multiplikation: *

Division und Brüche: /

Eingabe von Potenzen: **

Eingabe eines Kommas als Punkt: .

Eine Zelle ausführen: Enter und Shift gleichzeitig

Wurzeln: Quadratwurzeln: $\sqrt{x} =$ sqrt(x) und n-te Wurzeln: $\sqrt[n]{x} =$ x**(1/n)

$e$ -Funktion: $e^x =$ exp(x)

Logarithmen: ln(x) bzw. log(x)

Definition einer Variable $x$ : x=symbols('x')

Funktionen:

Zeichnen der Funktion $f(x) = x^2$ : plot(x**2)

Zeichnen der Funktion $f(x)=x^2$ im Intervall $[-2,10]$ : plot(x**2,(x,-2,10))

Egal, wo Sie sich im Notebook befinden: Wenn Sie Fragen zur Eingabe haben, können Sie einfach eine Zelle generieren, dort Spickzettel() eintragen und die Zelle durch gleichzeitiges Drücken der Shift und der Enter-Taste ausführen. Daraufhin erscheint noch einmal eine Liste mit Hinweisen, wie was eingegeben werden muss. Probieren Sie das gerne gleich einmal aus, indem Sie die nächste Zelle auführen.
Eine neue Zelle generieren Sie übrigens, indem Sie oben in der Symbolleiste auf das Plus-Zeichen klicken.

Spickzettel()

Warum Differentialrechnung?¶

Funktionen sind in der Natur und im Alltag allgegenwärtig. Um diese richtig analysieren und verstehen zu können, ist es sinnvoll, diese genau zu untersuchen, zum Beispiel im Hinblick auf Extrema, Änderungen, Grenzwerte... hier kommt die Differentialrechnung ins Spiel. Außerdem wird sie bei der Optimierung von Aufgaben benötigt.

Eine einfache Form der Optimierung haben Sie bereits vor sich, wenn Sie Ihren Garten gestalten wollen und eine möglichst große Fläche mit einer bestimmten Anzahl an Büschen begrenzen möchten.

Die Ableitung als momentane Änderungsrate¶

Die Ableitung einer Funktion $ f(x) $ an der Stelle $ x_0 $ gibt die Änderung der Funktion an der Stelle $ x_0 $ an. Sie stellt damit die momentane/lokale Änderungsrate dar und entspricht der Steigung der Tangente im Punkt $ (x_0|f(x_0)). $

Anschauliche Berechnung der Steigung in einem Punkt $(x_0|f(x_0))$ anhand einer Geraden.

Diese verläuft zunächst durch zwei Punkte: $(x_0|f(x_0))$ und einen weiteren Punkt, der von $(x_0|f(x_0))$ $\Delta x$ entfernt ist. Von links nach rechts wird $\Delta x$ immer kleiner.

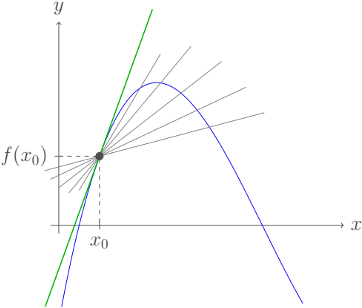
Genaue Beschreibung der Vorgehensweise anhand der Graphen von links nach rechts:

Eine Gerade schneidet den Graphen von $f$ in zwei Punkten, dies sind $(x_0|f(x_0))$ und $(x_0 + \Delta{x}| f(x_0 + \Delta{x}))$ .

Die Steigung der Geraden kann mit $m = \frac{\Delta{y}}{\Delta{x}} = \frac{f(x_0+\Delta{x}) - f(x_0)}{\Delta{x}}$ charakterisiert werden. Hier spricht man vom Differenzenquotienten.

Das $\Delta{x}$ wird verkleinert. Dadurch entsteht eine neue Gerade mit einer anderen Steigung, die aber wieder gleich bestimmt werden kann.

Das $\Delta{x}$ wird schrittweise weiter verkleinert. Dadurch entsteht jeweils eine neue Gerade mit einer anderen Steigung. Wird $\Delta{x}$ infinitesimal (unendlich) klein, so wird die Gerade eine Tangente und berührt den Graphen von $f$ in einem Punkt (grüne Gerade). Die Steigung dieser Tangente entspricht dann der Steigung des Graphen von $f$ im Punkt $x_0$ .

Wenn also $\Delta{x}$ gegen 0 geht, wir also den $lim$ für $\Delta{x} \rightarrow 0$ bilden, erhalten wir die 1. Ableitung der Funktion $f$ . Hier spricht man auch vom Differentialquotienten.

$f'(x_0) = \displaystyle \lim_{\Delta{x} \to 0} \frac{\Delta{y}}{\Delta{x}} = \displaystyle \lim_{\Delta{x} \to 0} \frac{f(x_0+\Delta{x}) - f(x_0)}{\Delta{x}}$

Aufgabe 1:¶

Machen Sie sich die anschauliche Bedeutung der momentanen Änderungsrate anhand der folgenden interaktiven Graphik klar.
Um die Graphik darzustellen, müssen Sie in die folgende Code-Zelle klicken und dann gleichzeit Shift und Enter drücken.
Die blaue Gerade schneidet den Graphen von $f(x) = (x+2)^2$ im Punkt $(0/4)$ und in einem weiteren Punkt. Stellen Sie den Regler so ein, dass die Gerade den Graphen lediglich im Punkt $(0/4)$ berührt. Am Schieberegler können Sie dann die Steigung des orangenen Graphen im Punkt $(0/4)$ ablesen. Sie entspricht der Steigung der blauen Geraden.

Mit einem Klick auf die Glühbirne erhalten Sie die Steigung im Punkt (0/4).

# Darstellen der interaktiven Graphik (gleichzeitig Shift und Enter drücken)
Demo.Differenzenquotient()

Alternative Form der Aufgabe, wenn Sie selbst etwas Code schreiben wollen:

Gehen Sie zum tieferen Verständnis der Ableitung als momentane Änderungsrate die folgenden Zellen Schritt für Schritt durch und erarbeiten Sie sich das Thema.

#Führen Sie die folgende Zelle aus. Dadurch wird f(x)=x**2 graphisch dargestellt.
from sympy import*
plot(x**2)

#Schreiben Sie nun selbst Code, um zwei Funktionen zu plotten.
#Die erste Funktion soll wieder f(x)=x**2 sein, die zweite g(x)=x
#Verwenden Sie den Befehl 'plot' von oben und fügen Sie in die Klammer mit einem Komma getrennt g(x) dazu.
#Führen Sie dann die Zelle aus.
#Hilfe erhalten Sie mit einem Klick auf die Glühbirne.
plot()       # Ergänzen Sie diese Zeile, damit f(x) und g(x) dargestellt werden.

Sehen Sie sich die Schaubilder der Funktionen an. Was hätten Sie für $g(x) = x$ erwartet? Sieht diese Funktion für Sie “komisch” aus? Wenn ja, woran liegt das?

#Plotten Sie die Funktion g(x)=x alleine (ohne die Funktion f(x)).
#Was ist der Unterschied zum oberen Plot?
#Klicken Sie anschließend auf die Glühbirne!
plot(x)

#Verschieben Sie nun die Funktion f(x)=x**2 um zwei Einheiten nach links.
#Diese neue Funktion nennen wir h(x).
#Plotten Sie anschließend die neue Funktion und nochmals die Funktion g(x)=x.
#Hilfe erhalten Sie wieder auf der Glühbirne.
plot()      # Ergänzen Sie diese Zeile, damit h(x) und g(x) dargestellt werden.

#Verschieben Sie nun g(x) um 8 Einheiten nach oben.
#Diese neue Funktion nennen wir k(x).
#Plotten Sie h(x) und k(x) in ein Schaubild.
#Tipps gibt es wieder auf der Glühbirne.
plot()     # Ergänzen Sie diese Zeile, damit h(x) und k(x) dargestellt werden.

Die Gerade schneidet den Graphen von $f(x)$ in zwei Punkten. Welche sind das? Berechnen Sie die beiden Schnittpunkte. Klicken Sie für die Lösung auf die Glühbirne.

Bestimmen Sie eine Funktion $j(x)$ , die wie $k(x)$ die Funktion $g(x)$ im Punkt $P(1|9)$ und in einem weiteren Punkt schneidet. Im Gegensatz zu $k(x)$ soll $j(x)$ die Steigung $m = 2$ haben.

Mit einem Klick auf die Glühbirne können Sie Ihre Geradengleichung kontrollieren. Auf dem Stift gibt es die ausführliche Rechnung.

#Plotten Sie nun h(x)= (x+2)**2 und j(x) in ein Schaubild.
#Wie verändert sich die Gerade?
#Werfen Sie dazu auch nochmal einen Blick auf die 4 Schaubilder zu Beginn des Notebooks.
plot()   # Ergänzen Sie diese Zeile, damit h(x) und j(x) dargestellt werden.

Bestimmen Sie nun eine Funktion $p(x)$ , die die Steigung $m= 6$ besitzt und die Funktion $g(x)$ im Punkt $P(1|9)$ berührt.

Mit einem Klick auf die Glühbirne können Sie Ihre Geradengleichung kontrollieren. Auf dem Stift gibt es die ausführliche Rechnung.

#Plotten Sie h(x) und p(x) in einem Schaubild
plot()     # Ergänzen Sie diese Zeile, damit h(x) und p(x) dargestellt werden.

Das Schaubild der Funktion $p(x)$ berührt die Funktion $h(x)$ im Punkt $P(1|9)$ . Die Steigung von $h(x)$ im Punkt $P(1|9)$ entspricht der Steigung der Tangenten in diesem Punkt. Die Steigung bzw. momentane Änderungsrate von $h(x)$ im Punkt $P(1|9)$ ist damit $m= 6$ .

Die Ableitung $f'(x)$ ist eine neue Funktion. Sie ordnet jedem Punkt $x$ die Steigung der ursprünglichen Funktion zu und beschreibt, “wie stark” sich die ursprüngliche Funktion ändert.

Schreibweisen der Ableitungsfunktion:

$ y' = f'(x) = \frac{dy}{dx} = \frac{df}{dx} = \frac{d}{dx}f(x) $

Um die Ableitungsfunktion zu bestimmen, kann direkt in den Differenzenquotienten eingesetzt und der Differentialquotient gebildet werden. Diese Rechnung ist recht aufwändig. Versuchen Sie es zum Verständnis trotzdem einmal mit der Funktion $f(x) = x^2$ . Machen Sie dazu den folgenden Ansatz:

$f'(x) = \displaystyle \lim_{\Delta{x} \to 0} \frac{(x+\Delta{x})^2 - (x^2)}{\Delta{x}}$

Behalten Sie im Auge, dass Sie als Ergebnis $f'(x) = 2x$ erhalten wollen.

Mit einem Klick auf die Glühbirne sehen Sie Details zur Rechnung.

Aufgaben¶

Generieren Sie sich zum Abschluss zur Übung die beiden folgenden weiteren Aufgaben, indem Sie jeweils in die Zelle klicken anschließend gleichzeitig Shift und Enter drücken.

Teil A¶

Differentialrechnung.Momentane_Aenderungsrate.Aufgabe(level=1)

Teil B¶

Differentialrechnung.Momentane_Aenderungsrate.Aufgabe(level=2)