book.mathe.studien.cloud

Rechenregeln¶

Diese Notebooks behandeln Zahlenmengen, deren Darstellung, das Rechnen mit Beträgen und binomischen Formeln und grundlegende mathematische Rechenregeln - Dinge, die Sie absolut beherrschen müssen!

Zahlenmengen, Intervalle und Beträge¶

Zahlenmengen

$\mathbb{N} = \{0,1,2,3,...\}$ Menge der natürlichen Zahlen

$\mathbb{Z} = \{...,-3,-2,-1,0,1,2,3,...\}$ Menge der ganzen Zahlen

$\mathbb{Q} = \{ \frac{p}{q}:p \in \mathbb{Z}, q \in \mathbb{Z} \setminus \{0\} \}$ Menge der rationalen Zahlen

$\mathbb{R}$ Menge der reellen Zahlen

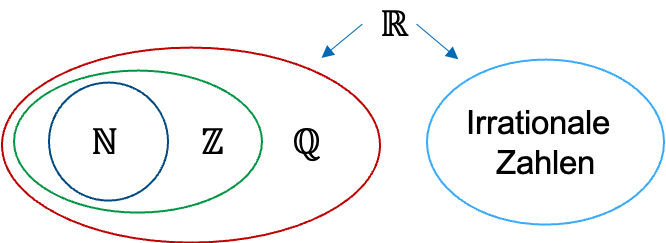
Die Menge der rationalen Zahlen zusammen mit der Menge der irrationalen Zahlen stellen die Menge der reellen Zahlen dar.

Rationale Zahlen: endliche oder periodische Dezimalzahlen

Beispiele:

$\frac{1}{2} = 0,5$

$\frac{7}{11} = 1,\overline{571428}$

$\frac{1}{3} = 0,\overline{3}$

Irrationale Zahlen: unendliche, nichtperiodische Dezimalzahlen

Beispiele:

$\sqrt{2} = 1,4142135...$

$\pi = 3,1415926...$

$\displaystyle{e} = 2,7182818...$

Darstellung auf der Zahlengeraden:

Intervalle

Intervalle sind Abschnitte der Zahlengerade.

$[a;b]:= \{x \in \mathbb{R} |\ a \le x \le b \}$ abgeschlossenes Intervall

$(a;b):= \{x \in \mathbb{R} |\ a < x < b \}$ offenes Intervall

$[a;b):= \{x \in \mathbb{R} |\ a \le x < b \}$ halboffenes Intervall

$(a;b]:= \{x \in \mathbb{R} |\ a < x \le b \}$ halboffenes Intervall

Spezialfälle: unendliche Intervalle

$(a;\infty):= \{x \in \mathbb{R}|\ a < x\}$

$(-\infty;b]:= \{x \in \mathbb{R}|\ x \le b\}$

$(-\infty,\infty):= \mathbb{R}$

Beispiele:

Im Video “Intervalle und Beträge” werden Intervalle nochmals mit Beispielen erklärt. Sie finden das Video unter: https://youtu.be/Swck7PCeY7E

Aufgabe¶

Generieren Sie sich nun Aufgaben zum Üben mit verschiedenen Schwierigkeitsstufen. Die Schwierigkeitsstufe ist dabei als Level jeweils in der Klammer angegeben. Führen Sie die folgenden Zellen aus, indem Sie jeweils in die Zelle klicken und gleichzeitig Shift und Enter drücken. Bearbeiten Sie dann die Aufgabe und tippen Sie Ihr Ergebnis zur Überprüfung ein.

Teil A¶

#Generiere Aufgabe mit Level 1 durch gleichzeitiges Drücken von Shift und Enter
Rechenregeln.Intervalle.Aufgabe(level=1)

#Generiere Aufgabe mit Level 2 durch gleichzeitiges Drücken von Shift und Enter
Rechenregeln.Intervalle.Aufgabe(level=2)

Beträge

Betrag einer Zahl $ a $: $ \vert{a}\vert $

$\vert{a}\vert$ : Abstand des Punktes $a \in \mathbb{R}$ auf der Zahlengeraden zur $0$

$ \vert{a - b} \vert $ ist der Abstand von $ a $ und $ b $ auf der Zahlengeraden.

$\left| a \right| = \left\{ \begin{array}{cll} \quad a \quad & \text{für} \quad & a > 0 \\ 0 & \text{für} & a=0 \\ -a & \text{für} & a < 0 \end{array} \right.$

$ = a $ für $ a > 0 $

$ \vert{a} \vert $ $ = 0 $ für $ a= 0 $

$= -a$ für $a < 0$