Dreisatz¶
Handwerkszeug für dieses Notebook:¶
Rechenoperationen:
Multiplikation: *
Division und Brüche: /
Eingabe von Potenzen: **
Eingabe eines Kommas als Punkt: .
Eine Zelle ausführen: Enter und Shift gleichzeitig
Egal, wo Sie sich im Notebook befinden: Wenn Sie Fragen zur Eingabe haben, können Sie einfach eine Zelle generieren, dort Spickzettel() eintragen und die Zelle durch gleichzeitiges Drücken der Shift- und der Enter-Taste ausführen. Daraufhin erscheint noch einmal eine Liste mit Hinweisen, wie was eingegeben werden muss. Probieren Sie das gerne gleich einmal aus, indem Sie die nächste Zelle ausführen.
# Generiere Spickzettel durch gleichzeitiges Drücken von Shift und Enter
Spickzettel()Wofür benötigt man Dreisatz?¶
Dreisatz benötigt man täglich: Zum Beispiel auf dem Markt. Ich möchte ein halbes Kilogramm Tomaten kaufen. Wie viel kostet das?

RDLAW @ Pixabay
Nehmen wir das Beispiel mit den Tomaten auf dem Bild und gehen systematisch vor. Ein Kilogramm kostet 3,99 €. Damit kostet ein halbes Kilogramm die Hälfte, also 1,995 €. Also vermutlich 1,99 €, wenn die kulante Verkäuferin hier etwas abrundet. 😉
Das ist hier recht schnell erkennbar. Bei “krummeren” Zahlen empfielt es sich, die gegebenen und gesuchten Daten in einer Tabelle aufzulisten. Gegebene Größen werden links geschrieben, gesuchte rechts:
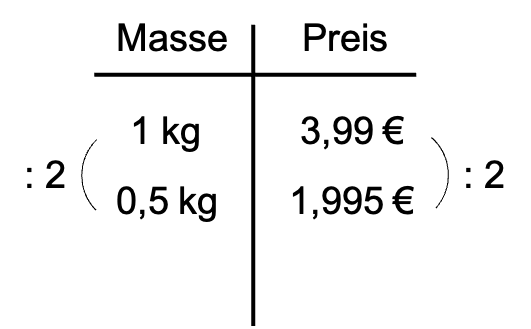
Gerader Dreisatz¶
Beispiel 2:
Was kosten 700 g Äpfel, wenn 500 g 2,50 € kosten?
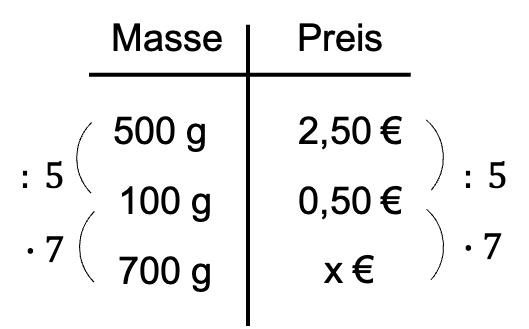
Die mathematische Formulierung und Berechnung ist folgendermaßen:
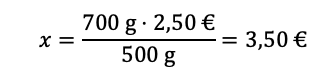
Zwei veränderliche Größen $G$ und $K$ heißen proportional, wenn sie immer im selben Verhältnis stehen.
( ist proportional zu )
d.h. .
Der gerade Dreisatz ist ein mathematisches Verhältnis, um aus drei gegebenen Werten eines Verhältnisses proportionaler Größen den unbekannten vierten Wert zu berechnen.
“Je mehr, desto mehr.”
Beispiel 3:
Die chemische Verbindung Natriummolybdat besitzt die molare Masse der Verbindung entsprechen einer Stoffmenge von etwa . Welcher Stoffmenge entsprechen Natriummolybdat?
Rechnen Sie selbst und klicken Sie für den Ergebnisabgleich auf die Glühbirne.
💡
Sie können zur Bestimmung des Ergebnisses den geraden Dreisatz verwenden.
20 \hspace{2mm} g \hspace{2mm} \widehat{=} \hspace{2mm} 0,097 \hspace{2mm} mol
75 \hspace{2mm} g \hspace{2mm} \widehat{=} \hspace{2mm} x \hspace{2mm} mol
x = \frac{0,097 \hspace{2mm} mol \hspace{2mm} \cdot \hspace{2mm} 75 \hspace{2mm} g}{20 \hspace{2mm} g} \approx 0,364 \hspace{2mm} mol
Alternativ ist es auch möglich, direkt mit dem Zusammenhang M = \frac{m}{n} zu rechnen.
\rightarrow n = \frac{75 \hspace{2mm} g}{205,92 \hspace{2mm} mol} = 0,364 \hspace{2mm}mol
Aufgaben¶
Generieren Sie sich nun Aufgaben zum Üben. Die Schwierigkeit der Aufgabe kann über das in Klammern angegebene Level gewählt werden. Führen Sie die folgende Zelle aus, indem Sie zunächst in die Zelle klicken und dann Steuerung und Enter gleichzeitig drücken. Berechnen Sie anschließend die Lösung der Aufgabe mit Stift und Papier und geben Sie das berechnete Ergebnis in das Textfeld ein. Durch Klicken auf den Button “Überprüfen” können Sie Ihr Ergebnis überprüfen. Wenn Sie nicht weiterkommen, dann klicken Sie auf die Glühbirne, um einen Tipp zu erhalten.
Teil A¶
# Generiere Aufgabe mit Schwierigkeitsstufe 1 durch gleichzeitiges Drücken von Steuerung und Enter
Dreisatz.Gerader_Dreisatz.Aufgabe(level=1)# Generiere Aufgabe mit Schwierigkeitsstufe 2 durch gleichzeitiges Drücken von Steuerung und Enter
Dreisatz.Gerader_Dreisatz.Aufgabe(level=2)Teil B¶
# Generiere Aufgabe mit Schwierigkeitsstufe 3 durch gleichzeitiges Drücken von Steuerung und Enter
Dreisatz.Gerader_Dreisatz.Aufgabe(level=3)Ungerader Dreisatz¶
Beispiel 4:
Beim Bau eines Hauses arbeiten 10 Handwerker an der Fertigstellung der Bäder. Bis alles erledigt ist, benötigen sie 10 Stunden. Wie lange benötigen 12 Arbeiter mit derselben Arbeitsleistung pro Person für die Fertigstellung?
Zunächst ein paar allgemeine Dinge zum ungeraden Dreisatz:
Zwei Größen $G$ und $K$ heißen antiproportional, wenn sie in einem entgegengesetzten Verhältnis zueinander stehen.
( ist proportional zu bzw. ist antiproportional zu )
d.h.
Der ungerade oder auch antiproportionale Dreisatz wird verwendet, wenn sich zwei Größen indirekt proportional zueinander verhalten. Hier wird aus drei gegebenen Werten antiproportionaler Größen der vierte Wert errechnet.
Wie beim geraden Dreisatz ist:
Die Berechnung erfolgt jedoch folgendermaßen:
“Je mehr desto weniger.”
Weiter mit Beispiel 4:

Mathematische Formulierung:
Arbeiter
Es werden damit etwas mehr als 8 Arbeitskräfte benötigt.
Beispiel 5:
Ein Teich soll zum Winter hin geleert werden. Dafür kommen Pumpen zum Einsatz. Geplant ist, 7 Pumpen zu verwenden. Betrachtet man deren Pumpleistung, dann benötigen die 7 Pumpen zusammen 3,5 Stunden, um den Teich leer zu pumpen. Im letzten Moment fallen 3 Pumpen aus. Wie lange dauert der Pumpvorgang dann, wenn nur 4 Pumpen zur Verfügung stehen?
Rechnen Sie selbst und klicken Sie für den Ergebnisabgleich auf die Glühbirne.
💡
Sie können zur Bestimmung des Ergebnisses den ungeraden Dreisatz verwenden.
7 \hspace{2mm} Pumpen \hspace{2mm} \widehat{=} \hspace{2mm} 3,5 \hspace{2mm} h
4 \hspace{2mm} Pumpen \hspace{2mm} \widehat{=} \hspace{2mm} x \hspace{2mm} h
x = \frac{3,5 \hspace{2mm} h \hspace{2mm} \cdot \hspace{2mm} 7 \hspace{2mm} Pumpen}{4 \hspace{2mm} Pumpen} = 6,125 \hspace{2mm} h
Aufgaben¶
Generieren Sie sich nun Aufgaben zum Üben. Die Schwierigkeit der Aufgabe kann über das in Klammern angegebene Level gewählt werden. Führen Sie die folgende Zelle aus, indem Sie zunächst in die Zelle klicken und dann Steuerung und Enter gleichzeitig drücken. Berechnen Sie anschließend die Lösung der Aufgabe mit Stift und Papier und geben Sie das berechnete Ergebnis in das Textfeld ein. Durch Klicken auf den Button “Überprüfen” können Sie Ihr Ergebnis überprüfen. Wenn Sie nicht weiterkommen, dann klicken Sie auf die Glühbirne, um einen Tipp zu erhalten.
# Generiere Aufgabe mit Schwierigkeitsstufe 1 durch gleichzeitiges Drücken von Steuerung und Enter
Dreisatz.Ungerader_Dreisatz.Aufgabe(level=1)# Generiere Aufgabe mit Schwierigkeitsstufe 2 durch gleichzeitiges Drücken von Steuerung und Enter
Dreisatz.Ungerader_Dreisatz.Aufgabe(level=2)